

共70分,把答案填在下面的横线上.)
1. 2. ___ 3.
20.(本题满分16分)已知在棱长为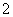 的正方体
的正方体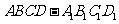 中,
中,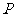 为棱
为棱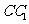 的中点,
的中点,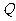 为正方形
为正方形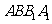 的中心,点
的中心,点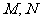 分别在直线
分别在直线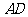 和
和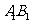 上.
上.
(1)若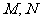 分别为棱
分别为棱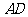 ,
,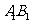 的中点,求直线
的中点,求直线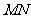 与
与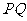 所成角的余弦值;
所成角的余弦值;
(2)若直线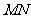 与直线
与直线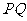 垂直相交,求此时线段
垂直相交,求此时线段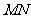 的长;
的长;
(3)在(2)的条件下,求直线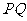 与
与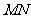 所确定的平面与平面
所确定的平面与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
审核:王斌 编校:王思亮
 2009-2010学年度第二学期期末考试
2009-2010学年度第二学期期末考试
高二数学答题纸(理科) 得分


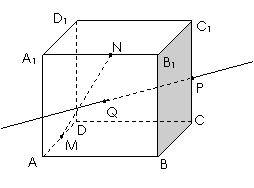
19.(本题满分16分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为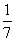 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用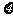 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(1)求袋中原有白球的个数;
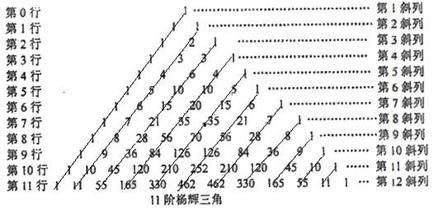
(2)求随机变量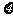 的概率分布;
的概率分布;
(3)求甲取到白球的概率.
18.(本题满分15分)杨辉是中国南宋末年的一位杰出的数学家、数学教育家,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第3个数;
(2)若第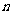 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为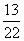 ,求
,求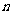 的值;
的值;
(3)写出第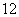 行所有数的和,写出
行所有数的和,写出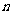 阶(包括
阶(包括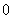 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35,我们发现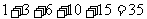 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第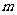 斜列中(从右上到左下)前
斜列中(从右上到左下)前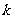 个数之和,一定等于第
个数之和,一定等于第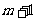 斜列中第
斜列中第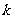 个数.
个数.
试用含有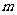 ,
,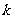
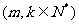 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.
17.(本题满分15分)甲、乙两人在罚球线投球命中的概率分别为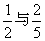 ,且各次投球相互之间没有影响.
,且各次投球相互之间没有影响.
(1)甲、乙两人在罚球线各投球一次,求这二次投球中恰好命中一次的概率;
(2)甲、乙两人在罚球线各投球二次,求这四次投球中至少有一次命中的概率.
16.(本题满分14分)已知直线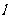 的参数方程为
的参数方程为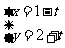 , 曲线
, 曲线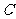 的极坐标方程为
的极坐标方程为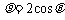 .
.
(1)将直线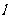 的参数方程化为普通方程;以极点为直角坐标系的原点,极轴为
的参数方程化为普通方程;以极点为直角坐标系的原点,极轴为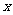 轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线
轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线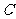 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若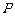 为直线
为直线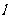 上任一点,
上任一点,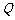 是曲线
是曲线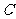 上任一点,求
上任一点,求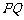 的最小值.
的最小值.
15.(本题满分14分) 已知复数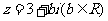 ,且
,且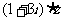 为纯虚数.
为纯虚数.
(1)求复数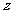 ;
;
(2)若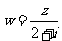 ,求复数
,求复数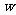 的模
的模 .
.
14.从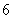 人中选
人中选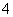 人分别到上海世博会美国馆、英国馆、法国馆、沙特馆四个馆参观,要求每个馆有一人参观,每人只参观一个馆,且这
人分别到上海世博会美国馆、英国馆、法国馆、沙特馆四个馆参观,要求每个馆有一人参观,每人只参观一个馆,且这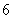 人中甲、乙两人不去法国馆参观,则不同的选择方案共有 ▲ 种.
人中甲、乙两人不去法国馆参观,则不同的选择方案共有 ▲ 种.
13.甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.5,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互之间没有影响.用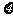 表示本场比赛的局数,则
表示本场比赛的局数,则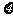 的数学期望为 ▲ .
的数学期望为 ▲ .
12.某射手进行射击训练,假设每次射击击中目标的概率为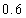 ,且各次射击的结果互不影响,则射手在
,且各次射击的结果互不影响,则射手在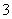 次射击中,恰有两次连续击中目标的概率是 ▲ .
次射击中,恰有两次连续击中目标的概率是 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com