
2.条件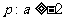 ;条件
;条件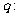
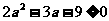 ,则
,则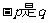 的 ( )
的 ( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分也非必要条件
1.集合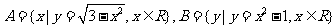 ,则A∩B= ( )
,则A∩B= ( )
A.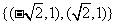 B.
B.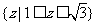
C. D.
D.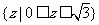
20.(本小题满分14分)
设动圆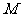 过点
过点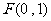 ,且与定圆
,且与定圆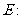
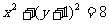 内切,动圆圆心
内切,动圆圆心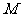 的轨迹记为曲线
的轨迹记为曲线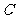 ,点
,点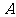 的坐标为
的坐标为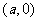 .
.
(1)求曲线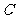 的方程;
的方程;
(2)若点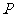 为曲线
为曲线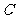 上任意一点,求点
上任意一点,求点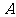 和点
和点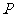 的距离的最大值
的距离的最大值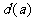 ;
;
(3)当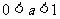 时,在(2)的条件下,设
时,在(2)的条件下,设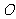 是坐标原点,
是坐标原点,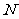 是曲线
是曲线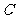 上横坐标为
上横坐标为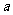 的点,记△
的点,记△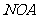 的面积为
的面积为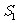 ,以
,以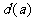 为边长的正方形的面积为
为边长的正方形的面积为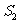 .若正数
.若正数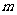 满足
满足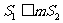 ,问
,问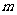 是否存在最小值?若存在,求出此最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出此最小值;若不存在,请说明理由.
19.(本小题满分14分)
已知函数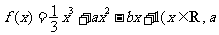 ,
,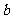 为实数)有极值,且在
为实数)有极值,且在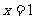 处的切线与直线
处的切线与直线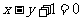 平行.
平行.
(1)求实数a的取值范围;
(2)设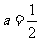 ,
,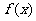 的导数为
的导数为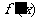 ,令
,令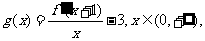
求证: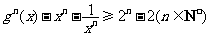 .
.
18.(本小题满分14分)
设等差数列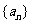 前
前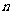 项和为
项和为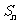 ,则有以下性质:
,则有以下性质: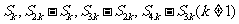 成等差数列.
成等差数列.
(1) 类比等差数列的上述性质,写出等比数列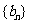 前
前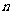 项积
项积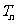 的类似性质;
的类似性质;
(2) 证明(1)中所得结论.
17.(本小题满分14分)
如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F
是CD的中点.
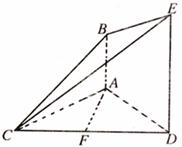 (1)求证:AF
(1)求证:AF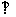 平面CDE;
平面CDE;
(2)求平面BCE与平面ACD所成锐二面角的大小.
16. (本小题满分12分)
第16届亚运会将于今年11月在我市举行,射击队运动员们正在积极备战. 若某运动员每次射击成绩为10环的概率为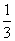 . 求该运动员在5次射击中,
. 求该运动员在5次射击中,
(1)恰有3次射击成绩为10环的概率;
(2)至少有3次射击成绩为10环的概率;
(3)射击成绩为10环的均值(数学期望).
(结果用分数表示)
15.(本小题满分12分)
已知函数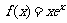 (
(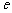 为自然对数的底).
为自然对数的底).
(1)求函数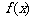 的单调区间; (2)求函数
的单调区间; (2)求函数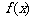 的极值.
的极值.
14.在10个球中有6个红球,4个白球(各不相同),不放回的依次摸出两个球,在第一次
摸出红球的条件下,第二次也摸出红球的概率是 .
13.在某项测量中,测量结果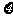 服从正态分布
服从正态分布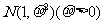 ,若
,若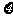 在
在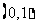 内取值的概率
内取值的概率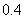 ,则
,则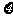 在
在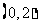 内取值的概率为
.
内取值的概率为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com