
22.(本小题满分14分)
已知点P是圆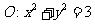 上动点,以点P为切点的切线与
上动点,以点P为切点的切线与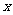 轴相交于点Q,直线OP与直线
轴相交于点Q,直线OP与直线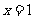 相交于点N,若动点M满足:
相交于点N,若动点M满足: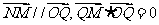 ,记动点M的轨迹为曲线C。
,记动点M的轨迹为曲线C。
(1)求曲线C的方程;
(2)若过点F(2,0)的动直线与曲线C相交于不在坐标轴上的两点A,B,设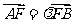 ,问在
,问在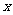 轴上是否存在定点E,使得
轴上是否存在定点E,使得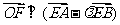 ?若存在,求出点E的坐标,若不存在,说明理由。
?若存在,求出点E的坐标,若不存在,说明理由。
21.(本小题满分12分)
已知函数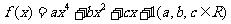 ,在
,在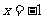 处取得极值
处取得极值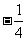 ,在
,在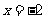 处的切线与直线
处的切线与直线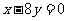 垂直。
垂直。
(1)求常数 的值;
的值;
(2)对于函数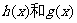 ,若存在常数
,若存在常数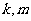 ,对于任意
,对于任意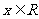 ,不等式
,不等式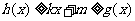 都成立,则称直线
都成立,则称直线 是函数
是函数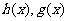 的分界线,求函数
的分界线,求函数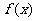 与函数
与函数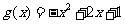 的“分界线”方程。
的“分界线”方程。
20.(本小题满分12分)
已知有穷数列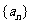 只有
只有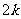 项(整数
项(整数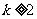 ),首项
),首项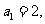 设该数列的前
设该数列的前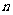 项和为
项和为 ,且
,且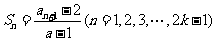 ,其中常数
,其中常数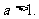
(1)求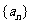 的通项公式;
的通项公式;
(2)若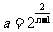 ,数列
,数列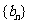 满足
满足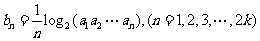 ,求证:
,求证: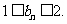
19.(本小题满分12分)
上海世博会即将开幕,某调查公司调查了南昌市某单位一办公室4位员工参观世博会意愿及消费习惯,得到结论如下表:
|
|
参观世博会的概率 |
参观世博会的消费金额(单位:元) |
|
员工1 |
 |
3000 |
|
员工2 |
 |
3000 |
|
员工3 |
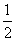 |
4000 |
|
员工4 |
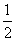 |
4000 |
(1)求这4位员工中恰好有2位员工参观世博会的概率;
(2)记这4位员工因参观世博会消费总金额不超过10000的概率。
18.(本小题满分12分)
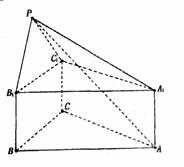 如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=1,点P在平面BCC1B1内,
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=1,点P在平面BCC1B1内,
(1)求证: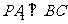 ;
;
(2)求二面角C1-PA1-A。
17.(本小题满分12分)
已知:函数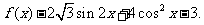
(1)求函数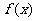 的最大值及此时
的最大值及此时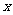 的值;
的值;
(2)在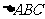 中,
中, 分别为内角A,B,C所对的边,且对
分别为内角A,B,C所对的边,且对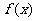 定义域中的任意的
定义域中的任意的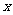 都有
都有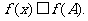 若
若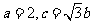 ,求
,求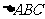 的面积。
的面积。
16.已知正四棱柱ABCD-A1B1C1D1的底面边长AB=6,侧棱长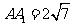 ,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,有以下判断,
,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,有以下判断,
(1)PE长的最大值是9;(2)三棱锥P-EBC的最大值是 ;(3)存在过点E的平面,裁球O的截面面积是
;(3)存在过点E的平面,裁球O的截面面积是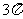 ;(4)三棱锥P-AEC1体积的最大值是20。
;(4)三棱锥P-AEC1体积的最大值是20。
正确的是 。
15.设函数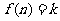 (其中
(其中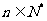 ),
),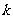 是
是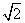 的小数点后第
的小数点后第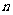 位数,则
位数,则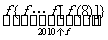 的值为
(
的值为
(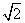 =1.41421356237…)
=1.41421356237…)
14.已知:向量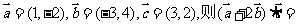 。
。
13.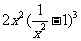 的展开式中常数项为
。(用数字作答)
的展开式中常数项为
。(用数字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com