

22、设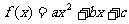 ,当
,当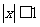 时,总有
时,总有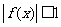 ,求证:
,求证: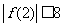 。
。
21、已知极坐标系的极点O与直角坐标系的原点重合,极轴与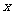 轴的正半轴重合,曲线
轴的正半轴重合,曲线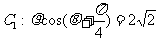 与曲线
与曲线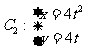 (参数
(参数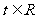 )交于A、B两点,
)交于A、B两点,
(1)求证: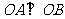 ;
;
(2)求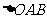 的外接圆的标准方程。
的外接圆的标准方程。
20、已知函数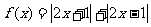 ,
,
(1)若对任意的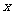 有
有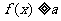 成立,求
成立,求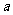 的取值范围;
的取值范围;
(2)若不等式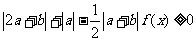 ,对于任意的
,对于任意的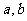 都成立,求
都成立,求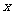 的取值范围。
的取值范围。
19、已知曲线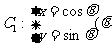 为参数),曲线
为参数),曲线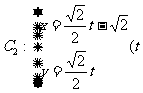 为参数)。
为参数)。
(1)指出 和
和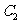 各是什么曲线,并说明
各是什么曲线,并说明 和
和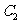 公共点的个数;
公共点的个数;
(2)若把 ,
,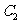 上各点的纵坐标都压缩为原来的一半,分别得到曲线
上各点的纵坐标都压缩为原来的一半,分别得到曲线 、
、 ,写出
,写出 ,
, 的参数方程。
的参数方程。 与
与 的公共点的个数和
的公共点的个数和 与
与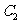 公共点的个数是否相同?说明你的理由。
公共点的个数是否相同?说明你的理由。
18、已知直线的极坐标方程为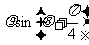 =
=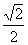 ,圆M的参数方程为
,圆M的参数方程为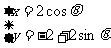 (其中
(其中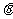 为参数)。
为参数)。
(1)将直线的极坐标方程化为直角坐标方程;
(2)求圆M上的点到直线的距离的最小值。
17、已知直线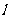 的参数方程为
的参数方程为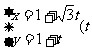 为参数),直线
为参数),直线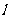 与曲线
与曲线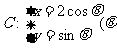 为参数)相交于两点A、B,求点P(1,1)到A、B两点的距离之积。
为参数)相交于两点A、B,求点P(1,1)到A、B两点的距离之积。
16、已知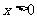 ,由不等式
,由不等式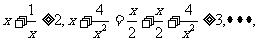 启发我们可以得到推广结论:
启发我们可以得到推广结论: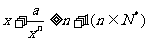 ,则
,则
15、圆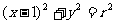 与椭圆
与椭圆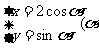 为参数)有公共点,则圆的半径的取值范围是
为参数)有公共点,则圆的半径的取值范围是
14、函数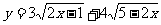 的最大值为
的最大值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com