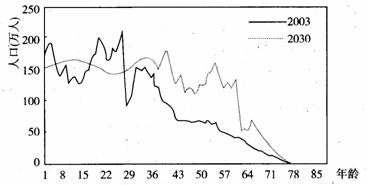
11．2030年与2003年相比，下列说法中最可能出现的是

A.出生率上升　　　　　 　B.死亡率上升

C．人口总数下降　　　　 D.自然增长率上升

　　　 读图5回答9-10题。

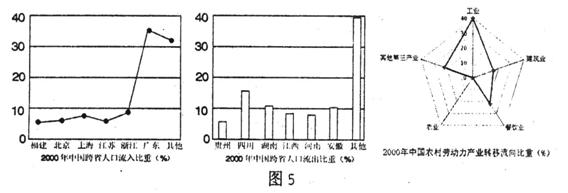
9．图中所示2000年中国人口流动特征是

①上海和江苏迁入人口之和与四川迁出人口大致相等　 ②农村劳动力向第三产业转移比重约为22%　 ③图中人口迁出的6个省份均位于地势第二级阶梯　 ④图中人口迁入的6个省份均位于东部经济地带　　

　 A．①②　　　 　　　　B．②③　 　　　　　　C．①④　　 　　　　D．②④

10．农村劳动力大量转移对迁入区的影响是

　 ①高城市化水平　 ②改善环境质量　 ③促进产业结构调整　 ④增加交通压力

　 A．①②③　 　　　　B．②③④ 　　　　　C．①②④　　　　 　D．①③④

读山东省2003年与2030年人口年龄结构比较图，完成11―12题。

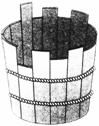读“木桶效应(组成木桶的木板如果长短不齐，那么这只木桶的盛水量，不取决于最长的那一块木板，而是取决于最短的那一块)图”，完成6-8题。

6.以某地的四类要素测得的各自所能供养的人口数量分别为8000、10000、6000、4500，则该地的环境承载力为

A. 8000　　　　　 B.10000　　　　 C.6000　　　　 　D.4500

7.如果用a表示本世纪初中国的人口数量，用b表示中国的人口合理容量，

用c表示中国的环境承载力，那么a、b、c三者的大小关系是

A.a<b<c　　　　　 B.c<b<a　　　 　　C.b<a<c　 　　　　D.a<c<b

8.下列影响我国不同省区人口合理容量的因素中相当于木桶短板的是

　　 A.四川--水力资源　　　　　　　　　　　　　 B.山东--气候资源

C.黑龙江--矿产资源　　　　　　　　 　　 D.内蒙古--水资源

截止2007年6月，世界人口已达64.77亿。下图表示除南极洲外的六大洲人口占世界总人口比例。读图回答4-5题。

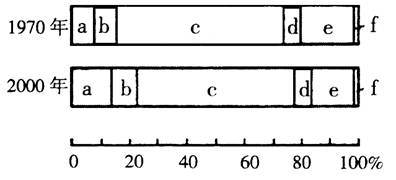
4．c大洲人口占世界总人口比例降低的主要原因是　　　

　A．主要国家的人口总量减少　　　　 　　　B．部分国家实行了计划生育政策

C．由于战争和灾害，人口死亡率上升　 　　D．人口大量迁出c大洲

5．e大洲的人口问题主要表现为　　　　　　　　　　　　　　　　　　　　　　　　　　

A．人口增长过多，人均资源不足　 　　　　　　 B．女性比例小，人口生育率低

C．人口素质低，缺乏环保意识　　 　　　　D．人口老龄化，劳动力不足

根据下表资料，回答1-3题。

我国四省(区)人口及部分自然资源统计数据表(2006年)

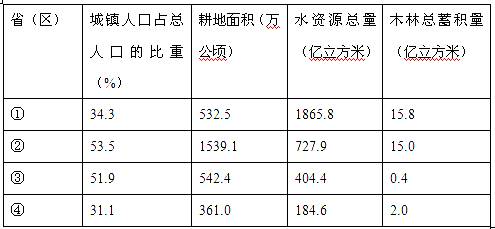
1. 表中①、②、③、④所示省(区)的简称依次是

A.川、黑、苏、陇 　　　B.苏、川、陇、黑　　 C.黑、川、陇、苏 D.陇、黑、川、苏

2．下列推理，其过程和结论正确的是

A．耕地面积①比②小，因此．山区面积①比②大

B．水资源总量②比③多，因此，年降水量②比③大

C．木材总蓄积量③比④少，因此，森林覆盖率③比④低

D．城镇人口占总人口比重①比③小，因此，乡村人口比重①比③大

3．有关四省(区)农业生产地叙述．正确的是　　

A．①省(区)西部是该省种植业集中地区

B．②省(区)东部是我国著名的棉花产区

C．③省(区)南部农业耕作制度一年三熟

D．④省(区)北部灌溉用水主要是地下水和高山冰雪融水

12．(2009年高考江苏卷)

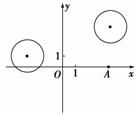
如图在平面直角坐标系xOy中，已知圆C₁：(x+3)²+(y－1)²＝4和圆C₂：(x－4)²+(y－5)²＝4.

(1)若直线l过点A(4,0)，且被圆C₁截得的弦长为2，求直线l的方程；

(2)设P为平面上的点，满足：存在过点P的无穷多对互相垂直的直线l₁和l₂，它们分别与圆C₁和C₂相交，且直线l₁被圆C₁截得的弦长与直线l₂被圆C₂截得的弦长相等，试求所有满足条件的点P的坐标．

解：(1)由于直线x＝4与圆C₁不相交，所以直线l的斜率存在．设直线l的方程为y＝k(x－4)，圆C₁的圆心到直线l的距离为d，因为直线l被圆C₁截得的弦长为2，所以d＝＝1.由点到直线的距离公式得d＝，从而k(24k+7)＝0，即k＝0或k＝－，所以直线l的方程为y＝0或7x+24y－28＝0.

(2)设点P(a，b)满足条件，不妨设直线l₁的方程为y－b＝k(x－a)，k≠0，则直线l₂的方程为y－b＝－(x－a)．因为圆C₁和圆C₂的半径相等，且直线l₁被圆C₁截得的弦长与直线l₂被圆C₂截得的弦长相等，所以圆C₁的圆心到直线l₁的距离和圆C₂的圆心到直线l₂的距离相等，即

＝，

整理得|1+3k+ak－b|＝|5k+4－a－bk|，从而1+3k+ak－b＝5k+4－a－bk或1+3k+ak－b＝－5k－4+a+bk，

即(a+b－2)·k＝b－a+3或(a－b+8)k＝a+b－5，因为k的取值有无穷多个，所以或解得或

这样点P只可能是点P₁(，－)或点P₂(－，)．

经检验点P₁和P₂满足题目条件．

11．(2010年江苏徐州调研)已知圆C的方程为x²+y²＝1，直线l₁过定点A(3,0)，且与圆C相切．

(1)求直线l₁的方程；

(2)设圆C与x轴交于P、Q两点，M是圆C上异于P、Q的任意一点，过点A且与x轴垂直的直线为l₂，直线PM交直线l₂于点P′，直线QM交直线l₂于点Q′.求证：以P′Q′为直径的圆C′总过定点，并求出定点坐标．

解：(1)∵直线l₁过点A(3,0)，且与圆C：x²+y²＝1相切，设直线l₁的方程为y＝k(x－3)，即kx－y－3k＝0，

则圆心O(0,0)到直线l₁的距离为d＝＝1，解得k＝±，

∴直线l₁的方程为y＝±(x－3)．

(2)对于圆C：x²+y²＝1，令y＝0，则x＝±1，即P(－1,0)，Q(1,0)．又直线l₂过点A且与x轴垂直，∴直线l₂方程为x＝3.

设M(s，t)，则直线PM的方程为y＝(x+1)．

解方程组得P′(3，)．同理可得Q′(3，)．

∴以P′Q′为直径的圆C′的方程为

(x－3)(x－3)+(y－)(y－)＝0，又s²+t²＝1，

∴整理得(x²+y²－6x+1)+y＝0，

若圆C′经过定点，只需令y＝0，从而有x²－6x+1＝0，解得x＝3±2，

∴圆C′总经过定点，定点坐标为(3±2，0)．

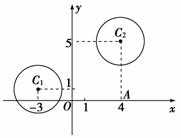
10．已知圆C₁：x²+y²+2x+2y－8＝0与圆C₂：x²+y²－2x+10y－24＝0相交于A、B两点，

(1)求公共弦AB所在的直线方程；

(2)求圆心在直线y＝－x上，且经过A、B两点的圆的方程．

解：(1)⇒x－2y+4＝0.

(2)由(1)得x＝2y－4，代入x²+y²+2x+2y－8＝0中得：y²－2y＝0.

∴或，即A(－4,0)，B(0,2)，

又圆心在直线y＝－x上，设圆心为M(x，－x)，则|MA|＝|MB|，解得M(－3,3)，∴⊙M：(x+3)²+(y－3)²＝10.

9．(2009年高考江西卷)设直线系M：xcosθ+(y－2)sinθ＝1(0≤θ≤2π)，对于下列四个命题：

A．存在一个圆与所有直线相交

B．存在一个圆与所有直线不相交

C．存在一个圆与所有直线相切

D．M中的直线所能围成的正三角形面积都相等

其中真命题的代号是________(写出所有真命题的代号)．

解析：xcosθ+ysinθ－2sinθ－1＝0.则点(0,2)到其直线的距离为

d＝＝1.

∴说明此直线是圆心为(0,2)，半径为1的圆的切线．

圆心为(0,2)，半径大于等于1的圆与所有直线相交，A对；

圆心为(0,2)，半径小于1的圆与所有直线不相交，B对；

圆心为(0,2)，半径等于1的圆与所有直线都相切，C对；

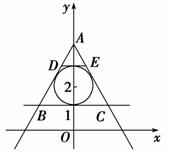
因为M中的直线与以(0,2)为圆心，半径为1的圆相切，所以M中的直线所能围成的正三角形面积不都相等．如图△ABC与△ADE均为等边三角形而面积不等．答案：A、B、C

8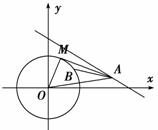．设圆O：x²+y²＝，直线l：x+3y－8＝0，点A∈l，使得圆O上存在点B，且∠OAB＝30°(O为坐标原点)，则点A的横坐标的取值范围是________．

解析：依题意点A∈l，设A(x₀，)．过点A作圆O的切线，切点为M，

则∠OAM≥∠OAB＝30°.从而sin∠OAM≥sin30°＝，即≥sin30°＝，就是|OA|²≤4(|OM|²)＝，x₀²+()²≤，5x₀²－8x₀≤0，解得x₀∈[0，]．

答案：[0，]