
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
D |
A |
C |
B |
A |
D |
C |
C |
B |
A |
C |
A |

(2)
 当
当 时,
时, 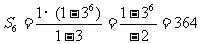
当 时,
时,


即(v-25)(v-64)<0,
解得25<v<64.
答:当v=40千米/小时,车流量最大,最大车流量约为

 千辆/小时.如果要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应大于25千米/小时且小于64千米/小时.
千辆/小时.如果要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应大于25千米/小时且小于64千米/小时.
22、(本小题14分)
解:(I)由 可得:
可得: 所以数列
所以数列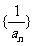 是等差数列,首项
是等差数列,首项 ,公差
,公差
∴ 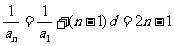
∴
(II)∵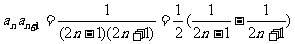
∴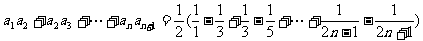
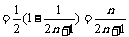
∴  解得
解得
解得n的取值范围:
22、(本小题14分)数列 满足
满足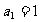 ,
, (
( )。
)。
(I)求证:数列 是等差数列;
是等差数列;
(II)若 ,求
,求 的取值范围。
的取值范围。
广德县实验中学、宣州区水阳高级中学2009-2010学年度第二学期期中考试两校联考 高一年级数学试卷参考答案
高一年级数学试卷参考答案
21、(本小题14分)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为: .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?(保留分数形式)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
20、(本小题12分)等差数列{an}不是常数列,a5=10,且a5,a7,a10是某一等比数列{bn}的第1,3,5项,
(1)求数列{an}的第20项;(2)求数列{bn}的通项公式。
19、(本小题满分12分)在等比数列 中,
中, ,
,
试求:(1)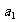 和公比
和公比 ;
;
(2)前6项的和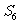 。
。
18、(本小题10分)已知不等式 的解集为
的解集为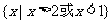
(1)求b和C的值;
(2)求不等式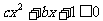 的解集。
的解集。
17、(本小题10分)已知a、b、c分别是 的三个内角A、B、C所对的边,若
的三个内角A、B、C所对的边,若 面积
面积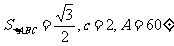 求
求 、b的值。
、b的值。
16、数列 1 ,
2
,
2 ,
3
,
3 ,
4
,
4 ,
5
,
5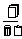 ,
…, 的前n项之和等于
,
…, 的前n项之和等于
 。
。
15、数列{ }的通项公式为
}的通项公式为 =2n-49,
=2n-49, 达到最小时,n等于______________。
达到最小时,n等于______________。
14、如果关于x的不等式 的解集为
的解集为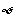 ,则实数a的取值范围是 。
,则实数a的取值范围是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com