
3.设a=(x1,y1),b=(x2,y2),则a b=
b= =x1x2+y1y2;其几何意义是a
=x1x2+y1y2;其几何意义是a b等于a的长度与b在a的方向上的投影的乘积;
b等于a的长度与b在a的方向上的投影的乘积;
2.两个向量垂直的充要条件, 设a=(x1,y1),b=(x2,y2),
(1)向量式:a⊥b(b≠0)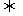 a
a b=0;
(2)坐标式:a⊥b
b=0;
(2)坐标式:a⊥b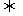 x1x2+y1y2=0;
x1x2+y1y2=0;
1.两个向量平行的充要条件,设a=(x1,y1),b=(x2,y2), 为实数。(1)向量式:a∥b(b≠0)
为实数。(1)向量式:a∥b(b≠0)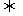 a=
a= b;(2)坐标式:a∥b(b≠0)
b;(2)坐标式:a∥b(b≠0)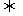 x1y2-x2y1=0;
x1y2-x2y1=0;
6.(1)正弦平方差公式:sin2A-sin2B=sin(A+B)sin(A-B);(2)三角形的内切圆半径r=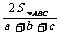 ;(3)三角形的外接圆直径2R=
;(3)三角形的外接圆直径2R=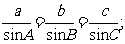
5.正弦型函数 的对称轴为
的对称轴为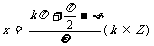 ;对称中心为
;对称中心为 ;类似可得余弦函数型的对称轴和对称中心;
;类似可得余弦函数型的对称轴和对称中心;
4.熟知正弦、余弦、正切的和、差、倍公式,正余弦定理,处理三角形内的三角函数问题勿忘三内角和等于1800,一般用正余弦定理实施边角互化;
3.记住同角三角函数的基本关系,熟练掌握三角函数的定义、图像、性质;
2.对于诱导公式,可用“奇变偶不变,符号看象限”概括;
1.三角函数符号规律记忆口诀:一全正,二正弦,三是切,四余弦;
11.若一阶线性递归数列an=kan-1+b(k≠0,k≠1),则总可以将其改写变形成如下形式: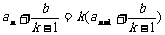 (n≥2),于是可依据等比数列的定义求出其通项公式;
(n≥2),于是可依据等比数列的定义求出其通项公式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com