
3.组合数性质: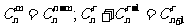 ;
;
2.组合数公式: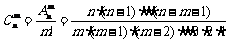 (m≤n),
(m≤n), ;
;
1.排列数公式: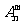 =n(n-1)(n-2)…(n-m+1)=
=n(n-1)(n-2)…(n-m+1)=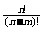 (m≤n,m、n∈N*),当m=n时为全排列
(m≤n,m、n∈N*),当m=n时为全排列 =n(n-1)(n-2)…3.2.1;
=n(n-1)(n-2)…3.2.1;
12.球的体积公式V=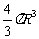 ,表面积公式
,表面积公式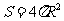 ;掌握球面上两点A、B间的距离求法:(1)计算线段AB的长,(2)计算球心角∠AOB的弧度数;(3)用弧长公式计算劣弧AB的长;
;掌握球面上两点A、B间的距离求法:(1)计算线段AB的长,(2)计算球心角∠AOB的弧度数;(3)用弧长公式计算劣弧AB的长;
11.欧拉公式:如果简单多面体的顶点数为V,面数为F,棱数为E.那么V+F-E=2;并且棱数E=各顶点连着的棱数和的一半=各面边数和的一半;
10.正方体和长方体的外接球的直径等与其体对角线长;
9.已知:长方体的体对角线与过同一顶点的三条棱所成的角分别为 因此有cos2
因此有cos2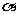 +cos2
+cos2 +cos2
+cos2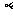 =1;
若长方体的体对角线与过同一顶点的三侧面所成的角分别为
=1;
若长方体的体对角线与过同一顶点的三侧面所成的角分别为 则有cos2
则有cos2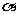 +cos2
+cos2 +cos2
+cos2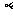 =2;
=2;
8.正棱锥的各侧面与底面所成的角相等,记为 ,则S侧cos
,则S侧cos =S底;
=S底;
7.空间距离的求法
(1)两异面直线间的距离,高考要求是给出公垂线,所以一般先利用垂直作出公垂线,然后再进行计算;
(2)求点到直线的距离,一般用三垂线定理作出垂线再求解;
(3)求点到平面的距离,一是用垂面法,借助面面垂直的性质来作,因此,确定已知面的垂面是关键;二是不作出公垂线,转化为求三棱锥的高,利用等体积法列方程求解;
6.二面角的求法
(1)定义法:直接在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线,得出平面角,用定义法时,要认真观察图形的特性;
(2)三垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;
(3)垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直;
(4)射影法:利用面积射影公式S射=S原cos ,其中
,其中 为平面角的大小,此方法不必在图形中画出平面角;
为平面角的大小,此方法不必在图形中画出平面角;
特别:对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其要考虑射影法)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com