
3.复数是纯虚数的条件: ①z=a+bi是纯虚数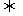 a=0且b≠0(a,b∈R); ②z是纯虚数
a=0且b≠0(a,b∈R); ②z是纯虚数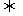 z+
z+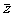 =0(z≠0);③z是纯虚数
=0(z≠0);③z是纯虚数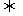 z2<0;
z2<0;
2.熟练掌握、灵活运用以下结论:(1)a+bi=c+di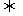 a=c且c=d(a,b,c,d∈R);(2)复数是实数的条件:①z=a+bi∈R
a=c且c=d(a,b,c,d∈R);(2)复数是实数的条件:①z=a+bi∈R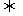 b=0
(a,b∈R);②z∈R
b=0
(a,b∈R);②z∈R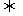 z=
z=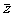 ;③z∈R
;③z∈R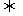 z2≥0;
z2≥0;
1.理解复数、实数、虚数、纯虚数、模、辐角、辐角主值、共轭复数的概念和复数的几何表示;
8.导数的应用:
(1)利用导数判断函数的单调性:设函数y=f(x)在某个区间内可导,如果 那么f(x)为增函数;如果
那么f(x)为增函数;如果 那么f(x)为减函数;如果在某个区间内恒有
那么f(x)为减函数;如果在某个区间内恒有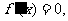 那么f(x)为常数;
那么f(x)为常数;
(2)求可导函数极值的步骤:①求导数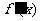 ;②求方程
;②求方程 的根;③检验
的根;③检验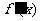 在方程
在方程 根的左右的符号,如果左正右负,那么函数y=f(x)在这个根处取得最大值;如果左负右正,那么函数y=f(x)在这个根处取得最小值;
根的左右的符号,如果左正右负,那么函数y=f(x)在这个根处取得最大值;如果左负右正,那么函数y=f(x)在这个根处取得最小值;
(3)求可导函数最大值与最小值的步骤:①求y=f(x)在(a,b)内的极值;②将y=f(x)在各极值点的极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个是最小值。
7.复合函数的导数:
6.常见函数的导数公式: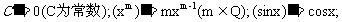
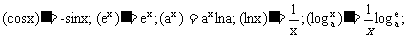
5.导数的四则运算法则: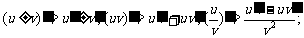
4.导数的几何意义:曲线y=f(x)在点P(x0,f(x0))处的切线的斜率是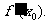 相应地,切线方程是
相应地,切线方程是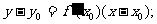
3.可导与连续的关系:如果函数y=f(x)在点x0处可导,那么函数y=f(x)在点x0处连续;但是y=f(x)在点x0处连续却不一定可导;
2.根据导数的定义,求函数的导数步骤为:
(1)求函数的增量
(2)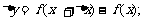 (2)求平均变化率
(2)求平均变化率 ;
;
(3)取极限,得导数 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com