
2.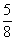 ;
;
3.(2010四川宜宾)
某班举行演讲革命故事的比赛中有一个抽奖活动.活动规则是:进入最后决赛的甲、乙两位同学,每人只有一次抽奖机会,在如图所示的翻奖牌正面的4个数字中任选一个数字,选中后可以得到该数字后面的奖品,第一人选中的数字,第二人就不能再选择该数字.
(1)求第一位抽奖的同学抽中文具与计算器的的概率分别是多少?
(2)有同学认为,如果.甲先抽,那么他抽到海宝的概率会大些,你同意这种说法吗?
并用列表格或画树状图的方式加以说明.

答案:1.(3);
2.(2010山东德州)袋子中装有3个红球和5个白球,这些球除颜色外均相同.在看不到球的条件下,随机从袋中摸出一个球,则摸出白球的概率是_____________.
1.(2010四川宜宾)
下列三种说法:
(1)三条任意长的线段都可以组成一个三角形;
(2)任意掷一枚均匀的硬币,正面一定朝上;
(3)购买一张彩票可能中奖.
其中,正确说法的序号是
2.(2010昆明)如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有数字1、3、6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).
(1)请用画树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果;
 (2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.
(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.
解:(1)
列表如下: 树形图如下:
|
|
1 |
3 |
6 |
|
1 |
(1 ,1) |
(1 ,3) |
(1 ,6) |
|
3 |
(3 ,1) |
(3 ,3) |
(3 ,6) |
|
6 |
(6 ,1) |
(6 ,3) |
(6 ,6) |
备注:此小题4分,画对表1(或图1)得2分,结果写对得2分.
 表1:
图1:
表1:
图1:
|
|
1 |
3 |
6 |
|
1 |
|
|
|
|
3 |
|
|
|
|
6 |
|
|
|
(2)数字之和分别为:2,4,7,4,6,9,7,9,12.
算术平方根分别是: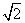 ,2,
,2, ,2,
,2,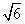 ,3,
,3, ,3,
,3, ………………5分
………………5分
设两数字之和的算术平方根为无理数是事件A
∴ ………………8分
………………8分
1.(2010山东济南)
如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内分别标有数字1、2、-3、-4.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇形内).
请你用列表法或树状图求a与 b的乘积等于2的概率.

.解:a与b的乘积的所有可能出现的结果如下表所示:
|
1 |
2 |
-3 |
-4 |
||
|
1 |
1 |
2 |
-3 |
-4 |
||
|
2 |
2 |
4 |
-6 |
-8 |
||
|
-3 |
-3 |
-6 |
9 |
12 |
||
|
-4 |
-4 |
-8 |
12 |
16 |
········································································································· 6分
总共有16种结果,每种结果出现的可能性相同,其中ab=2的结果有2种,
·················································································································· 7分
∴a与 b的乘积等于2的概率是 . ······················································ 8分
. ······················································ 8分
2.(2010黄冈)(6分)甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.
(1)求满足关于x的方程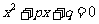 有实数解的概率.
有实数解的概率.
(2)求(1)中方程有两个相同实数解的概率.
解:两人投掷骰子共有36种等可能情况.(1)其中方程有实数解共有19种情况,故其概率为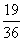 。(2)方程有相等实数解共有2种情况,故其概率为
。(2)方程有相等实数解共有2种情况,故其概率为 。
。
1.(2010宁德)下列事件是必然事件的是( ).C
A.随意掷两个均匀的骰子,朝上面的点数之和为6
B.抛一枚硬币,正面朝上
C.3个人分成两组,一定有2个人分在一组
20.解:
 |
A |
A |
A |
B |
B |
C |
|
A |
(A, A) |
(A, A) |
(A, A) |
(A, B) |
(A, B) |
(A, C) |
|
A |
(A, A) |
(A, A) |
(A, A) |
(A, B) |
(A, B) |
(A, C) |
|
A |
(A, A) |
(A, A) |
(A, A) |
(A, B) |
(A, B) |
(A, C) |
|
B |
(B, A) |
(B, A) |
(B, A) |
(B, B) |
(B, B) |
(B, C) |
|
B |
(B, A) |
(B, A) |
(B, A) |
(B, B) |
(B, B) |
(B, C) |
|
C |
(C, A) |
(C, A) |
(C, A) |
(C, B) |
(C, B) |
(C, C) |

 所有可能的结果:
所有可能的结果:
(A, A) (A, A) (A, A) (A, A) (A, A) (A, A) (B, A) (B, A) (B, A) (B, A) (C, A) (C, A)
(A, A) (A, B) (A, A) (A, B) (A, A) (A, B) (B, A) (B, B) (B, A) (B, B) (C, A) (C, B)
(A, B) (A, C) (A, B) (A, C) (A, B) (A, C) (B, B) (B, C) (B, B) (B, C) (C, B) (C, C)
列出表格或画出树状图得----------------- -----4分
 -----------------------6分
-----------------------6分
(2010山西7.在一个不透明的袋中,装有若干个除颜色不同外其余都相同的球,如果袋中有3个红球且摸到红球的概率为 ,那么袋中球的总个数为()B
A.15个 B.12个 C.9个 D.3个
(2010山西13.随意地抛一粒豆子,恰好落在图中的方格中(每个方格除颜外完全一样),那么这粒豆子停在黑色方格中的概率是______________.


(2010山西16.哥哥与弟弟玩一个游戏:三张大小、质地都相同的卡片上分别标有数字1、2、3.将标有数字的一面朝 下,哥哥从中任意抽取一张,记下数字后放回洗匀,然后弟弟从中任意抽取一张,计算抽得的两个数字之和,如果和为奇数,则弟弟胜;和为偶数,则哥哥胜该游戏对双方______________(填“公平”或“不公平”).不公平
22.(2010陕西省)某班毕业联欢会设计的即兴表演节目的摸球游戏,游戏采用一个不透明的盒子,里面装有五个分别标有数字1、2、3、4、5的乒乓球,这些球出书字外,其他完全相同,游戏规则是参加联欢会的50名同学,每人将盒子乒乓球摇匀后闭上眼睛从中随即一次摸出两个球(每位同学必须且只能摸一次)。若两球上的数字之和是偶数就给大家即兴表演一个节目;否则,下个同学接着做摸球游戏依次进行。
(1)用列表法或画树状图法求参加联欢会同学表演即兴节目的概率
(2)估计本次联欢会上有多少个同学表演即兴节目?
解:(1)如下表:
|
两数和 |
1 |
2 |
3 |
4 |
5 |
|
1 |
|
3 |
4 |
5 |
6 |
|
2 |
3 |
|
5 |
6 |
7 |
|
3 |
4 |
5 |
|
7 |
8 |
|
4 |
5 |
6 |
7 |
|
9 |
|
5 |
6 |
7 |
8 |
9 |
|
从上表可以看出,一次性共有20种可能结果,其中两数为偶数的共有8种。将参加联欢会的某位同学即兴表演节目记为事件A
∴P(A)=P(两数和为偶数)=8/20=2/5
(2)∵50×2/5=20(人)
∴估计有20名同学即兴表演节目。
(2010年天津市)(15)甲盒装有3个乒乓球,分别标号为1,2,3;乙盒装有2个乒乓球,分别标号为1,2.现分别从每个盒中随机地取出1个球,则取出的两球标号之和为4的概率是  .
.
(2010宁夏20.(6分)
在一个不透明的盒子里,装有3个写有字母A、2个写有字母B和1个写有字母C的小球, 它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下字母后放回盒子,摇匀后再随机取出一个小球,记下字母.请你用画树状图或列表的方法,求摸出的两个小球上分别写有字母B、C的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com