
5.(陕西卷理10文10)某学校要召开学生代表大会,规定各班每10人推选一名代表 ,当各班人数除以10的余数大于6时再增选一名代表,那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]( [x]表示不大于x的最大整数)可以表示为 [ ]
A.  B.
B. 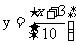 C.
C.  D.
D. 
[答案]B
[解析](方法一)当 除以
除以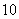 的余数为
的余数为 时,由题设知
时,由题设知 ,且易验证知此时
,且易验证知此时 ,当
,当 除以
除以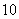 的余数为
的余数为 时,由题设知
时,由题设知 ,且易验证知此时
,且易验证知此时 ,故综上知,必有
,故综上知,必有 ,故选
,故选 .
.
4.(山东卷理11文11)函数y=2x-x2的图像大致是

[答案]A
[解析]因为当x=2或4时,2x  -
- =0,所以排除B、C;当x=-2时,2x
=0,所以排除B、C;当x=-2时,2x  -
- =
=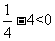 ,故排除D,所以选A。
,故排除D,所以选A。
[命题意图]本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力。
3.(全国Ⅰ新卷理11文12)已知函数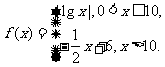 若
若 互不相等,且
互不相等,且 则
则 的取值范围是
的取值范围是
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
[答案]C
解析:不妨设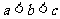 ,取特例,如取
,取特例,如取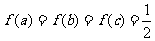 ,则易得
,则易得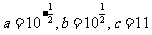 ,从而
,从而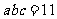 ,选C.
,选C.
另解:不妨设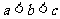 ,则由
,则由 ,再根据图像易得
,再根据图像易得 ,故选C.
,故选C.
2.(湖南卷理8)用 表示a,b两数中的最小值。若函数
表示a,b两数中的最小值。若函数 的图像关于直线x=
的图像关于直线x= 对称,则t的值为
对称,则t的值为
A.-2 B.2 C.-1 D.1 
[命题意图]本题通过新定义考察学生的创新能力,考察函数的图象,考察考生数形结合的能力,属中档题。
1.(福建卷理4文7)函数 的零点个数为
的零点个数为
A.0 B.1 C.2 D.3
[答案]C
[解析]当 时,令
时,令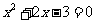 解得
解得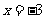 ;
;
当 时,令
时,令 解得
解得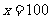 ,所以已知函数有两个零点,选C。
,所以已知函数有两个零点,选C。
[命题意图]本题考查分段函数零点的求法,考查了分类讨论的数学思想。
21.(本小题满分13分)
已知
(1)若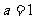 ,求
,求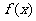 的极小值;
的极小值;
(2)是否存在实数 ,使
,使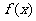 的最小值为3。
的最小值为3。
20.(本小题满分13分)
设椭圆 的左、右焦点分别为F1、F2,过椭圆C上的一点A作
的左、右焦点分别为F1、F2,过椭圆C上的一点A作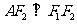 ,又坐标原点O到直线AF1的距离为
,又坐标原点O到直线AF1的距离为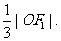
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过Q的直线 交
交 轴于点P(-1,0),交
轴于点P(-1,0),交 轴于点M,若
轴于点M,若 ,求直线
,求直线 的方程。
的方程。
19.(本小题满分13分)
某公司进行技术改造的可行性分析,在未来10年内准备向银行贷款进行技术创新。现有两种贷款方案可供选择。
方案1:一次性贷款10万元,第一年获利1万元,以后每年比前一年增加30%的利润;
方案2:每年贷款1万元,第一年获利1万元,以后每年比前一年增加5千元利润;
两种方案都是10年后一次性归还本息,若银行两种形式的贷款都按年息5%的复利计算,请你帮助该公司作出合理化选择,并说明理由。
(取 )
)
18.(本小题满分12分)
如图,四边形ABCD是正方形, 平面ABCD,MA//PB,PB=AB=2MA=2。
平面ABCD,MA//PB,PB=AB=2MA=2。
 (1)P、C、D、M四点是否在同一平面内,为什么?
(1)P、C、D、M四点是否在同一平面内,为什么?
(2)求证:面PBD 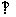 面PAC;
面PAC;
(3)求多面体PABCDM的体积。
17.(本小题满分12分)
某家政服务公司根据用户满意度将本公司家政服务员分为两类,其中A类12名、B类 名。
名。
(1)若采用分层抽样的方式随机抽取20名家政服务员参加技术培训,抽取到的B类人数是16,求 的值;
的值;
(2)某客户来公司聘请3名家政服务员,但是由于公司人员安排已经接近饱和,只有甲、乙、丙、丁、戊五人可供选择,请列出该客户的所有可能选择的情况,并求该客户最终聘请了丙但没聘请乙的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com