
8.矩阵 的逆矩阵是 .
的逆矩阵是 .
7.在椭圆中,我们有如下结论:椭圆 上斜率为1的弦的中点在直线
上斜率为1的弦的中点在直线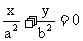 上,类比上述结论,得到正确的结论为:双曲线
上,类比上述结论,得到正确的结论为:双曲线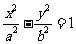 上斜率为1的弦的中点在直线 上.
上斜率为1的弦的中点在直线 上.
6. 的展开式中的第六项是
.
的展开式中的第六项是
.
5.一射击运动员对同一目标独立地射击四次,,若此射击运动员每次射击命中的概率为,则至少命中一次的概率为 .
4.若 ,其中
,其中 、
、
 ,
, 使虚数单位,则
使虚数单位,则 .
.
3.已知a=(2,4,5), b=(3,6,y),若a∥b,则 y= .
2. 人排成一排照相,要求甲排在两端,不同的排法共有________种.(用数字作答)
人排成一排照相,要求甲排在两端,不同的排法共有________种.(用数字作答)
1.设复数z满足z=3+4i(其中i为虚数单位),则z的模为_____.
19。(1)f(x)=|x|(x-a)
当a=0时,f(x)=x·|x|为奇函数
当a≠0时,f(x)=(x-a)|x|,∵f(-a)≠f(a)且f(-a)≠-f(a)
∴f(x)是非奇非偶函数……………………(5分)
(2)当a=0时,f(x)=x|x|是奇函数,在R上单调递增
∴当-1≤x≤ 时,f(-1)≤f(x)≤f(
时,f(-1)≤f(x)≤f( )
) f(x)∈[-1,
f(x)∈[-1, ],此时f(x)max=
],此时f(x)max=
当a<0时, ………………………………(7分)
………………………………(7分)
即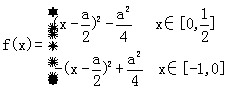 ……………………………………(10分)
……………………………………(10分)
①若-1≤ 即a≥-2时,f(x)的最大值为f(
即a≥-2时,f(x)的最大值为f( )或f(
)或f( )
)
∵f( )-f(
)-f( )=
)=
又∵-2≤a<0,则f( )<f(
)<f( ),∴f(
),∴f( )为最大值……………………(14分)
)为最大值……………………(14分)
所以f(x)的最大值为f( )=
)= 。16分
。16分
20[解](Ⅰ)由题意: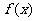 的定义域为
的定义域为 ,且
,且 .
.
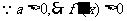 ,故
,故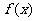 在
在 上是单调递增函数. 6分
上是单调递增函数. 6分
(Ⅱ)由(1)可知: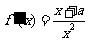
① 若 ,则
,则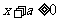 ,即
,即 在
在 上恒成立,此时
上恒成立,此时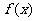 在
在 上为增函数,
上为增函数,

 (舍去)9分
(舍去)9分
② 若 ,则
,则 ,即
,即 在
在 上恒成立,此时
上恒成立,此时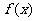 在
在 上为减函数,
上为减函数,

 所以,
所以,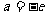 13分
13分
③ 若 ,令
,令 得
得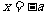 ,
,
当 时,
时, 在
在 上为减函数,
上为减函数,
当 时,
时, 在
在 上为增函数,
上为增函数,
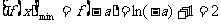
 综上可知:
综上可知:  16分
16分
 淮安市淮阴区2009-2010学年度第二学期期末高二年级调查测试
淮安市淮阴区2009-2010学年度第二学期期末高二年级调查测试
19.(本题满分14分)
已知函数f(x)=|x|(x-a),(a∈R).
(1)讨论f(x)在R上的奇偶性;
(2)当a≤0时,求函数f(x)在闭区间[-1, ]上的最大值.
]上的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com