8．(2010株洲市)如图所示的正方形网格中，网格线的交点称为格点．已知、是两格点，如果也是图中的格点，且使得为等腰三角形，则点的个数是

A．6　　　　　　　　　　　　　 B．7　　　　　　　　　　　　　　 C．8　　　　　　　　　　　 D．9

4．证明：(1)∵BE＝CF，

∴BE+EF＝CF+EF，　　 …………1分

即BF＝CE．　　 …………………2分

又∵∠A＝∠D，∠B＝∠C，

∴△ABF≌△DCE(AAS)，　　　　 ……………………………………4分

∴AB＝DC．　　　　　　　　　　 ………………………………………5分

(2)△OEF为等腰三角形　　　　　 …………………………………6分

理由如下：∵△ABF≌△DCE，

∴∠AFB=∠DEC．

∴OE=OF．

∴△OEF为等腰三角形．　　　　　　 …………………………………8分

3、解：△ABD是等腰三角形．………………………………………………………………l分

在BD上取点E，使BE=AC，连接AE，

∵AC∥BD，BE = AC，

∴四边形ACBE是平行四边形．………………………………………………… 3分

又∵∠C = 90°

∴四边形ACBE是矩形． …………………………………………………………5分

∴AE⊥BD．…………………………………………………………………………6分

又∵BE = AC = BD，……………………………………………………………7分

∴BE = ED．

∴AB=AD．　 ……………………………………………………………………… 8分

故△ABD是等腰三角形．

2、证明：∵ CE⊥AD于E，BF⊥AD于F，

∴∠CED =∠BFD =90°．　　 …………………………………………………l分

又∵AD是BC边上的中线，

∴BD =CD．　 …………………………………………………………………2分

又∵∠BDF=∠CDE，　　 ………………………………………………………3分

∴△BDF≌△CDE．　 …………………………………………………………4分

故BF=CE．　　　　 …………………………………………………………5分

4．(2010山东德州)

如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．

(1)求证：AB＝DC；

(2)试判断△OEF的形状，并说明理由．

答案：1． 2;

3、(2010四川宜宾)

已知：如图，在Rt△ABC中，∠C=90°，过点B作BD∥AC，且BD=2AC，连接AD．

试判断△ABD的形状，并说明理由．

2、 (2010四川宜宾)如图，分别过点C、B作△ABC的BC边上的中线AD及其延长线的垂线，垂足分

别为E、F．求证：BF=CE．

1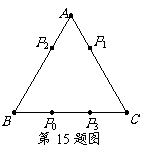．(2010山东德州)电子跳蚤游戏盘是如图所示的△ABC，AB=AC=BC=6．如果跳蚤开始时在BC边的P₀处，BP₀=2．跳蚤第一步从P₀跳到AC边的P₁(第1次落点)处，且CP₁= CP₀；第二步从P₁跳到AB边的P₂(第2次落点)处，且AP₂= AP₁；第三步从P₂跳到BC边的P₃(第3次落点)处，且BP₃= BP₂；…；跳蚤按照上述规则一直跳下去，第n次落点为P_n(n为正整数)，则点P₂₀₀₉与点P₂₀₁₀之间的距离为_________．

17．(2010昆明)如图，点B、D、C、F在一条直线上，且BC = FD，AB = EF.

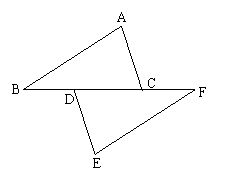(1)请你只添加一个条件(不再加辅助线)，使△ABC≌△EFD，你添加的条件是　　　　　　　　 ；

(2)添加了条件后，证明△ABC≌△EFD.

答案：(1)∠B = ∠F　或　AB∥EF　或　AC = ED.　　　　　　　　　 ………………2分

　(2)证明：当∠B = ∠F时

　　 在△ABC和△EFD中

　　 　　　　　　　　　　　………………5分

　　 ∴△ABC≌△EFD 　(SAS) 　　　…………………6分

(本题其它证法参照此标准给分)

23．(2010山东济南)

已知：△ABC是任意三角形．

⑴如图1所示，点M、P、N分别是边AB、BC、CA的中点．求证：∠MPN=∠A．

⑵如图2所示，点M、N分别在边AB、AC上，且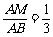，，点P₁、P₂是边BC的三等分点，你认为∠MP₁N+∠MP₂N=∠A是否正确？请说明你的理由．

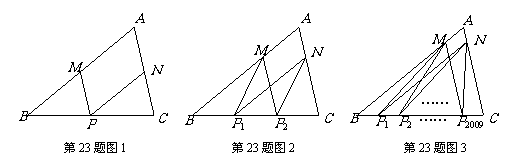⑶如图3所示，点M、N分别在边AB、AC上，且，，点P₁、P₂、……、P₂₀₀₉是边BC的2010等分点，则∠MP₁N+∠MP₂N+……+∠MP₂₀₀₉N=____________．

(请直接将该小问的答案写在横线上．)

答案：23. ⑴证明：∵点M、P、N分别是AB、BC、CA的中点，

　　　 　　∴线段MP、PN是△ABC的中位线，

∴MP∥AN，PN∥AM，················· 1分

　　 　　∴四边形AMPN是平行四边形，····· 2分

　　 　　　∴∠MPN=∠A.　 ·························· 3分

⑵∠MP₁N+∠MP₂N=∠A正确.　 ················· 4分

如图所示，连接MN，　 ························· 5分

∵，∠A=∠A，

∴△AMN∽△ABC，

∴∠AMN=∠B，，

∴MN∥BC，MN=BC，　 ····················· 6分

∵点P₁、P₂是边BC的三等分点，

∴MN与BP₁平行且相等，MN与P₁P₂平行且相等，MN与P₂C平行且相等，

∴四边形MBP₁N、MP₁P₂N、MP₂CN都是平行四边形，

∴MB∥NP₁，MP₁∥NP₂，MP₂∥AC，

································································· 7分

∴∠MP₁N=∠1，∠MP₂N=∠2，∠BMP₂=∠A，

∴∠MP₁N+∠MP₂N=∠1+∠2=∠BMP₂=∠A.

······························································· 8分

⑶∠A.　 ················································ 9分