
3.(湖北卷文19)已知某地今年年初拥有居民住房的总面积为a(单位:m2),其中有部分旧住房需要拆除。当地有关部门决定每年以当年年初住房面积的10%建设新住房,同事也拆除面积为b(单位:m2)的旧住房。
(Ⅰ)分别写出第一年末和第二年末的实际住房面积的表达式:
(Ⅱ)如果第五年末该地的住房面积正好比今年年初的住房面积增加了30%,则每年拆除的旧住房面积b是多少?(计算时取1.15=1.6)

2.(福建卷文17)数列{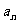 } 中
} 中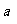 =
=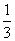 ,前n项和
,前n项和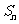 满足
满足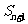 -
-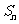 =
= (n
(n
 ).
).
( I ) 求数列{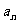 }的通项公式
}的通项公式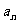 以及前n项和
以及前n项和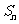 ;
;
(II)若S1, t ( S1+S2 ), 3( S2+S3 ) 成等差数列,求实数t的值。


1. (安徽卷文21)设
(安徽卷文21)设 是坐标平面上的一列圆,它们的圆心都在
是坐标平面上的一列圆,它们的圆心都在 轴的正半轴上,且都与直线
轴的正半轴上,且都与直线 相切,对每一个正整数
相切,对每一个正整数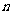 ,圆
,圆 都与圆
都与圆 相互外切,以
相互外切,以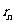 表示
表示 的半径,已知
的半径,已知 为递增数列.
为递增数列.
(Ⅰ)证明: 为等比数列;
为等比数列;
(Ⅱ)设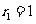 ,求数列
,求数列 的前
的前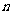 项和.
项和.
[命题意图]本题考查等比列的基本知识,利用错位相减法求和等基本方法,考察抽象概括能力以及推理论证能力.
[解题指导](1)求直线倾斜角的正弦,设 的圆心为
的圆心为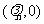 ,得
,得 ,同理得
,同理得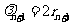 ,结合两圆相切得圆心距与半径间的关系,得两圆半径之间的关系,即
,结合两圆相切得圆心距与半径间的关系,得两圆半径之间的关系,即 中
中 与
与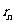 的关系,证明
的关系,证明 为等比数列;(2)利用(1)的结论求
为等比数列;(2)利用(1)的结论求 的通项公式,代入数列
的通项公式,代入数列 ,然后用错位相减法求和.
,然后用错位相减法求和.


[方法技巧]对于数列与几何图形相结合的问题,通常利用几何知识,并结合图形,得出关于数列相邻项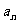 与
与 之间的关系,然后根据这个递推关系,结合所求内容变形,得出通项公式或其他所求结论.对于数列求和问题,若数列的通项公式由等差与等比数列的积构成的数列时,通常是利用前n项和
之间的关系,然后根据这个递推关系,结合所求内容变形,得出通项公式或其他所求结论.对于数列求和问题,若数列的通项公式由等差与等比数列的积构成的数列时,通常是利用前n项和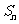 乘以公比,然后错位相减解决.
乘以公比,然后错位相减解决.
1.(辽宁卷理16)已知数列 满足
满足 则
则 的最小值为_________
的最小值为_________ _.
_.

 (三)解答题(共14题)
(三)解答题(共14题)
2.(江西卷理5)等比数列 中,
中, ,
, =4,函数
=4,函数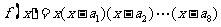 ,则
,则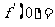 ( )
( )
A. B.
B. 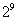 C.
C.  D.
D. 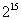
[答案]C
[解析]考查多项式函数的导数公式,重点考查学生创新意识,综合与灵活地应用所学的数学知识、思想和方法。考虑到求导中,含有x项均取0,则 只与函数
只与函数 的一次项有关;得:
的一次项有关;得: 。
。
1.(湖北卷文7)已知等比数列{ }中,各项都是正数,且
}中,各项都是正数,且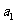 ,
,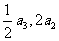 成等差数列,则
成等差数列,则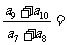
A. B.
B.  C.
C.
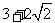 D
D
[答案]C

7、 (2008上海市浦东新区第一学期期末质量抽测)
(2008上海市浦东新区第一学期期末质量抽测)
某工程的工序流程如图所示. 若该工程总时数
为9天,则工序d的天数x最大为__________.
答案 4
6、(2008江苏省姜堰中学阶段性考试)
若执行右面的程序图的算法,
则输出的p=_______

答案 2550
5、(2008江苏省省阜中高三第三次调研考试数学(文科)试题)
如图给出的是计算 的值的一个程序框图,
的值的一个程序框图,
其中判断框内应填入的条件是 .
答案 
4、(2008山东省潍坊市高三教学质量检测)
如图所示的程序框图输出的结果是 ( )

A. B.
B.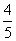 C.
C. D.
D.
答案 C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com