
2.双向约束问题
物体(如小球)在轻杆作用下的运动,或在管道中运动时,随着速度的变化,杆或管道对其弹力发生变 化.这里的弹力可以是支持力,也可以是压力,即物体所受的弹力可以是双向的,与轻绳的模型不同.因为绳子只能提供拉力,不能提供支持力;而杆、管道既可以提供拉力,又可以提供支持力;在管道中运动,物体速度较大时可对上壁产生压力,而速度较小时可对下壁产生压力.在强力为零时即出现临界状态.
化.这里的弹力可以是支持力,也可以是压力,即物体所受的弹力可以是双向的,与轻绳的模型不同.因为绳子只能提供拉力,不能提供支持力;而杆、管道既可以提供拉力,又可以提供支持力;在管道中运动,物体速度较大时可对上壁产生压力,而速度较小时可对下壁产生压力.在强力为零时即出现临界状态.
 (一)轻杆模型
(一)轻杆模型
如图所示,轻杆一端连一小球,在竖直面内作圆周运动.
(1)能过最高点的临界条件是: .这可理解为恰好转过或恰好不能转过最高点的临界条件,此时支持力
.这可理解为恰好转过或恰好不能转过最高点的临界条件,此时支持力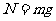 .
.
(2)当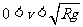 时,
时,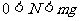 ,N仍为支持力,且N随v的增大而减小,
,N仍为支持力,且N随v的增大而减小,
(3)当 时,N=0,此为轻杆不受弹力的临界条件.
时,N=0,此为轻杆不受弹力的临界条件.
(4)当 时,N随
时,N随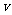 的增大而增大,且N为拉力指向圆心,
的增大而增大,且N为拉力指向圆心,
[例4] 如图所示,被长L的轻杆连接的小球A能绕固定点O在竖直平面内作圆周运动,O点竖直高度为h,如杆受到的拉力等于小球所受重力的5倍时,就会断裂,则当小球运动的角速度为多大时,杆恰好断裂?小球飞出后,落地点与O点的水平距离是多少?

 ㈡管道模型
㈡管道模型
质点(小球)在光滑、竖直面内的圆管中作圆周运动(圆管截面半径r远小于球的圆周运动的半径R),如图所示.小球达到最高点时对管壁的压力有三种情况:
(1)刚好对管壁无压力,此时重力为向心力,临界速度为 .
.
(2)当 时,对下管壁有压力,此时
时,对下管壁有压力,此时 ,故
,故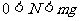 。
。
(3)当 时,对上管壁有压力,此时
时,对上管壁有压力,此时 。
。
实际上,轻杆和管道两种约束情况可化归为同类的物理模型,即双向约束模型.
[例5] 一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多).在细管中有两个直径与细管内径相同的小球(可视为质点),A球的质量为m1,B球的质量为m2,它们沿环形圆管顺时针运动,经过最低点时的速度都为V0。设A球运动到最低点时,B球恰好运动到最高点,若要此时两球作用于圆管的合力为零,那么ml,m2,R与V0所满足的关系式是 ·
[例6] 一根内壁光滑的细圆管放在竖直面内,如图所示,一小钢球自A口的正上方距A口高h处无初速释放,第1次小球恰能抵达B点,第2次落入A口后从B射出,恰能再进入A口,则两次小球下落的高度之比 。
。

1.临界速度问题
在变速圆周运动中的某些特殊位置上,常存在着最小(或最大)的速度,小于(或大于)这个速度,物体就不能再继续作圆周运动了,此速度即为临界速度.在这个位置,物体的受力必满足特定的条件,这就是临界条件.当物体的受力发生变化时,其运动状态随之变化.当某力突然变为零时,对应物体出现相应的临界状态.常见的如绳子突然断裂、支持物的作用力突然变化、静摩擦力充当向心力时突然消失或达最大值等.通过受力分析来确定临界状态和临界条件,是较常用的解题方法.
(1)没有支持物的质点(如绳系小球),在竖直面内的圆周运动的最高点:
(1)受力至少应是重力mg,此即为向心力的最小值.由 ,得临界速度
,得临界速度 ,此速度是质点恰好能通过最高点的条件.
,此速度是质点恰好能通过最高点的条件.
(2)当 时,质点可通过最高点;当
时,质点可通过最高点;当 时,质点不能运动到最高点,在达到最高点之前就已经脱离了圆轨道.
时,质点不能运动到最高点,在达到最高点之前就已经脱离了圆轨道.
(3)在水平转台上作圆周运动的物体,静摩擦力f提供向心力.当转台的转速逐渐增大时,静摩擦力随之增大,f达到最大值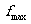 时,对应有临界角速度和临界速度.
时,对应有临界角速度和临界速度.
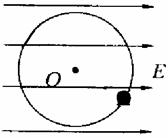
[例1] 组成星球的物质是靠引力吸引在一起的,这样的星球有一个最大的自转速率.如果超过了该速率,星球的万有引力将不足以维持其赤道附近的物体做圆周运动.由此能得到半径为R、密度为ρ、质量为M且均匀分布的星球的最小自转周期T,下列表达式中正确的是( )
A.  B.
B.
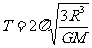
C.  D.
D.

[例2] 如图所示,LMPQ是光滑轨道,LM水平,长为5.0m,MPQ是一半径为R=1.6m的半圆,QOM在同一竖直线上,在恒力F作用下质量m=1kg的物体A由静止开始运动,当达到M时立即停止用力,欲使A刚能通过Q点,则力F大小是多大?

[例3] 如图所示,竖直放置的光滑圆环,半径为R,要使质量为m小球沿环内侧做完整的圆周运动(如过山车),那么,小球在最低点的速度V0至少为多大?

①若在原题的基础上,使小球带正电荷g,在空间加一匀强电场,若所加电场方向竖直向下,如图所示,则小球在最高点不脱离圆轨道的最小速度应满足什么条件?
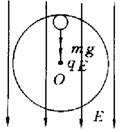
②如图所示,若所加电场方向水平向右,则小球在什么地方具有最小速度才能在圆轨道上做完整的圆周运动,其最小速度是多少?
3.解答圆周运动问题时的注意事项
(1)圆周运动的轨道平面、圆心位置和半径;
(2)确定是匀速圆周运动还是变速圆周运动,以确定运用相应的物理规律;
(3)正确进行受力分析,并进行相应的分解(一般是沿法向和切向进行正交分解),再根据牛顿第二定律沿半径方向列出动力学方程;
(4)注意圆周运动问题中的临界状态及临界条件的确定,结合能量的观点来求解.
2.变速圆周运动的动力学特征
(1)受合外力作用,但合力并不总是指向圆心,且合力的大小也是可以变化的,故合力可对物体做功,物体的速率也在变化.
(2)合外力的分力(在某些位置上也可以是合外力)提供向心力.
1.匀速圆周运动的动力学特征
(1)始终受合外力作用,且合外力提供向心力,其大小不变,始终指向圆心,因合力始终与速度垂直,所以合力不做功.
(2)匀速圆周运动的动力学方程
根据题意,可以选择相关的运动学量如v,ω,T,f列出动力学方程; ,
, ,
, 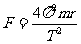 ,
,  .
.
熟练掌握这些方程,会给解题带来方便.
20. 用“我们”作开头,重组下面这个句子,不能改变原意。(6分)
书籍将人类自身无法逾越的障碍和局限揭示给我们,而且毫不保留地将人的痛苦、幸福、愉悦、悲伤、烦恼、绝望、矛盾等种种复杂的心理启示给我们。
我们____________________________________________________。
19. 下面这则请假条中存在语言不得体、不简明的问题,请把不得体的词语和不简明之处找出来,分别写在相应的横线上。(6分)
黄老师:
下周一,广东体院将在我市举行面试,作为具有着良好身体素质、体育成绩卓著的学生,届时我将出席这次考试。为此,我特意向您专门请假一天,请您务必批准。
此致
敬礼!
学生 李翔
2010年6月20日
(1)不得体的词语(4个):
(2)不简明之处(2处):
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com