5．向量概念的教学应从物理背景和几何背景入手，物理背景是力、速度、加速度等概念，几何背景是有向线段。了解这些物理背景和几何背景，对于学生理解向量概念和运用向量解决实际问题都是十分重要的。教师还可以引导学生运用向量解决一些物理和几何问题。例如，利用向量计算力使物体沿某方向运动所做的功，利用向量解决平面内两条直线平行与垂直的位置关系等问题。对于向量的非正交分解只要求学生作一般了解，不必展开。

4．弧度是学生比较难接受的概念，教学中应使学生体会弧度也是一种度量角的单位(圆周的1/2π所对的圆心角或周角的1/2π)。随着后续课程的学习，他们将会逐步理解这一概念，在此不必深究。

3．提醒学生重视学科之间的联系与综合，在学习其他学科的相关内容(如单摆运动、波的传播、交流电)时，注意运用三角函数来分析和理解。

2．在三角函数的教学中，应发挥单位圆的作用。单位圆可以帮助学生直观地认识任意角、任意角的三角函数，理解三角函数的周期性、诱导公式、同角三角函数关系式，以及三角函数的图象和基本性质。借助单位圆的直观，教师可以引导学生自主地探索三角函数的有关性质，培养他们分析问题和解决问题的能力。

1．在三角函数的教学中，教师应根据学生的生活经验，创设丰富的情境，使学生体会三角函数模型的意义。例如，通过单摆、弹簧振子、圆上一点的运动，以及音乐、波浪、潮汐、四季变化等实例，使学生感受周期现象的广泛存在，认识周期现象的变化规律，体会三角函数是刻画周期现象的重要模型(参见例1)。

3．三角恒等变换(约8课时)

　(1)经历用向量的数量积推导出两角差的余弦公式的过程，进一步体会向量方法的作用。

　(2)能从两角差的余弦公式导出两角和与差的正弦、余弦、正切公式，二倍角的正弦、余弦、正切公式，了解它们的内在联系。

　(3)能运用上述公式进行简单的恒等变换(包括引导导出积化和差、和差化积、半角公式，但不要求记忆)。

　说明与建议

2．平面向量(约12课时)

　(1)平面向量的实际背景及基本概念

　通过力和力的分析等实例，了解向量的实际背景，理解平面向量和向量相等的含义，理解向量的几何表示。

　(2)向量的线性运算

　① 通过实例，掌握向量加、减法的运算，并理解其几何意义。

　② 通过实例，掌握向量数乘的运算，并理解其几何意义，以及两个向量共线的含义。

　③ 了解向量的线性运算性质及其几何意义。

　(3)平面向量的基本定理及坐标表示

　① 了解平面向量的基本定理及其意义。

　② 掌握平面向量的正交分解及其坐标表示。

　③ 会用坐标表示平面向量的加、减与数乘运算。

　④ 理解用坐标表示的平面向量共线的条件。

　(4)平面向量的数量积

　① 通过物理中“功”等实例，理解平面向量数量积的含义及其物理意义。

　② 体会平面向量的数量积与向量投影的关系。

　③ 掌握数量积的坐标表达式，会进行平面向量数量积的运算。

　④ 能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系。

　(5)向量的应用

　经历用向量方法解决某些简单的平面几何问题、力学问题与其他一些实际问题的过程，体会向量是一种处理几何问题、物理问题等的工具，发展运算能力和解决实际问题的能力。

1．三角函数(约16课时)

　(1)任意角、弧度

　了解任意角的概念和弧度制，能进行弧度与角度的互化。

　(2)三角函数

　①借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义。

　②借助单位圆中的三角函数线推导出诱导公式(π/2±α, π±α的正弦、余弦、正切)，能画出y=sin x, y=cos x, y=tan x的图象，了解三角函数的周期性。

　③借助图象理解正弦函数、余弦函数在[0，2π]，正切函数在(-π/2，π/2)上的性质(如单调性、最大和最小值、图象与x轴交点等)。

　④理解同角三角函数的基本关系式：sin²x+cos²x=1，sin x/cos x=tan x。

　⑤结合具体实例，了解y=Asin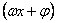的实际意义；能借助计算器或计算机画出y=Asin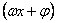的图象，观察参数A，ω，对函数图象变化的影响。

　⑥会用三角函数解决一些简单实际问题，体会三角函数是描述周期变化现象的重要函数模型。

8．古典概型的教学应让学生通过实例理解古典概型的特征：实验结果的有限性和每一个实验结果出现的等可能性。让学生初步学会把一些实际问题化为古典概型。教学中不要把重点放在"如何计数"上。