17．(玉溪市2010)在玉溪州大河旁边的路灯杆顶上有一个物体，它的抽象几何图形如图8，

若, 求B、C两点间的距离.

解：过A点作AD⊥BC于点D，　　　　　　　　　　　　　　　　　 …………1分

在Rt△ABD中，∵∠ABC=60°，∴∠BAD=30°.　　　　　　　　 …………2分

∵AB=4,

∴BD=2,　 ∴AD=2.　　　　　　　　　　　　　　　　　　　 …………4分　　　　　　　

在Rt△ADC中，AC=10，

∴CD===2 .　　　　　　　　　　　　 　…………5分

∴BC=2+2　 .　　　　　　　　　　　　　　　　　　　　　 …………6分

答：B、C两点间的距离为2+2.　　　　　　　　　　　　　 …………7分

19．(2010台州市)施工队准备在一段斜坡上铺上台阶方便通行．现测得斜坡上铅垂的两

棵树间水平距离AB=4米，斜面距离BC=4.25米，斜坡总长DE=85米．

(1)求坡角∠D的度数(结果精确到1°)；

(2)若这段斜坡用厚度为17cm的长方体台阶来铺，需要铺几级台阶?

解：19．(8分)(1) cos∠D=cos∠ABC=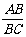=0.94，　 ………………………………… 3分

∴∠D20°．　　 ………………………………………………………………………1分

(2)EF=DEsin∠D=85sin20°85×0.34=28.9(米) ，　 ……………………………3分

共需台阶28.9×100÷17=170级．　　 ………………………………………………1分

17.(2010红河自治州)(本小题满分9分)如图5，一架飞机在空中P处探测到某高山山顶D处的俯角为60°，

此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行，飞行10秒到山顶D的正上方C处，此时测得飞机距地平面的垂直高度为12千米，求这座山的高(精确到0.1千米)

解：延长CD交AB于G，则CG=12(千米)

依题意：PC=300×10=3000(米)=3(千米)

在Rt△PCD中：

PC=3，∠P=60°

CD=PC·tan∠P

　 =3×tan60°

　 =

∴12-CD=12-≈6.8(千米)

答：这座山的高约为6.8千米.

　　 (2010遵义市)(10分)如图,水坝的横断面是梯形,背水坡AB的坡

角∠BAD=,坡长AB=,为加强水坝强度,

将坝底从A处向后水平延伸到F处,使新的背水坡

的坡角∠F=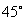,求AF的长度(结果精确到1米,

参考数据: ,).

　 答案：(10分)解：过B作BE⊥AD于E

　　　　　　　　　　　　　　　 在Rt△ABE中,∠BAE=,　　∴∠ABE=

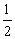　　　　　　　　　　　　　　　　 ∴AE＝AB

　　　　　　　　　　　　　　　 ∴BE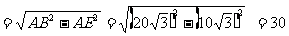

　　　　　　　　　　　　　　　 ∴在Rt△BEF中, ∠F＝,　　∴EF＝BE＝30

　　　　 　　　　　　　 ∴AF＝EF－AE＝30－

　　　　　　　　　　　 ∵，　　∴AF＝12.6813

13.(2010红河自治州) 计算：+2sin60°= 　　　

8. 尽管有许多的困难，他还是决定独自面对。(in spite of)

7. 一旦有一天我们用完了自然资源，后果无法想象。(run out of)

6. 他的表演给观众留下了深刻的印象。(impress)

5. 如果我的老师现在在这里，他就会告诉我该做什么

4. 等车的时候，他看到一个老朋友经过但那个人没有注意到他。

3. 他来广州的目的是要找到更好的工作。(aim)_K^S*5U.C#