
1、设 则
则 ( )
( )
A. B.
B.
C. D.
D.
2、设集合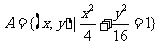 ,
,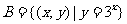 ,则
,则 的元素个数是( )
的元素个数是( )
A.4 B.3 C .2 D.1
3、对于实数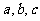 ,“
,“ ”是“
”是“ ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.(2010,浙江义乌)如图1,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.
(1)如图2,当BP=BA时,∠EBF= ▲ °,猜想∠QFC= ▲ °;
(2)如图1,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明;
(3)已知线段AB=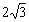 ,设BP=
,设BP= ,点Q到射线BC的距离为y,求y关于
,点Q到射线BC的距离为y,求y关于 的函数关系式.
的函数关系式.




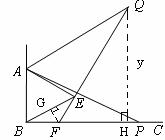
图3
[答案](1)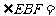 30°.
30°. =
60°
=
60°
(2) =60°
=60°
 不妨设BP>
不妨设BP> , 如图1所示
, 如图1所示
∵∠BAP=∠BAE+∠EAP=60°+∠EAP
∠EAQ=∠QAP+∠EAP=60°+∠EAP
∴∠BAP=∠EAQ
在△ABP和△AEQ中 AB=AE,∠BAP=∠EAQ, AP=AQ
∴△ABP≌△AEQ(SAS)
∴∠AEQ=∠ABP=90°
∴∠BEF
∴ =∠EBF +∠BEF =30°+30°=60°
=∠EBF +∠BEF =30°+30°=60°
(事实上当BP≤ 时,如图2情形,不失一般性结论仍然成立,不分类讨论不扣分)(3) 在图1中,过点F作FG⊥BE于点G
时,如图2情形,不失一般性结论仍然成立,不分类讨论不扣分)(3) 在图1中,过点F作FG⊥BE于点G
∵△ABE是等边三角形
∴BE=AB= ,由(1)得
,由(1)得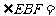 30°
30°
在Rt△BGF中, ∴BF=
∴BF= ∴EF=2
∴EF=2
∵△ABP≌△AEQ ∴QE=BP= ∴QF=QE+EF
∴QF=QE+EF
过点Q作QH⊥BC,垂足为H
在Rt△QHF中, (x>0)
(x>0)
即y关于x的函数关系式是:
5.(2010,浙江义乌) 如图,以线段 为直径的⊙
为直径的⊙ 交线段
交线段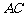 于点
于点 ,点
,点 是弧AE的中点,
是弧AE的中点, 交
交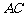 于点
于点 ,
,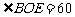 °,
°,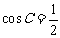 ,
, .
.
(1)求 的度数;
的度数;
(2)求证:BC是⊙ 的切线;
的切线;
(3)求MD的长度.


[答案]解:(1)∵∠BOE=60°
∴∠A = ∠BOE = 30°
∠BOE = 30°
(2) 在△ABC中
∵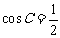 ∴∠C=60°
∴∠C=60°
又∵∠A =30°
∴∠ABC=90°∴ ∴BC是⊙
∴BC是⊙ 的切线
的切线
(3)∵点M是弧AE的中点 ∴OM⊥AE
在Rt△ABC中 ∵ ∴AB=
∴AB=
∴OA=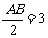
∴OD=
 ∴MD=
∴MD=
4.(2010,浙江义乌)(1)计算: °
°
(2)化简:
[答案](1)原式=1+2-1
=2
(2)原式=
=
=
3.(2010,安徽芜湖)图1为已建设封顶的16层楼房和其塔吊图,图2为其示意图,吊臂AB与地面EH平行,测得A点到楼顶D点的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地面,EF=16m,求塔吊的高CH的长.

[答案]解:根据题意得:DE=3.5×16=56,AB=EF=16
∵∠ACB=∠CBG-∠CAB=15°,
∴∠ACB =∠ CAB
∴CB=AB=16.
∴CG=BCsin30°=8
CH=CG+HG=CG+DE+AD=8+56+5=69.
∴塔吊的高CH的长为69m.
2.(2010,安徽芜湖)17.(1)计算:(-1)2010×(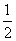 )-3+│
)-3+│ -4cos60°│
-4cos60°│
[答案]解:原式=1×8+1+│ -2│
-2│
=8+1+2-
=11-
1.(2010,浙江义乌)课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的投影BC长为24米,则旗杆AB的高度约是 ▲ 米.(结果保留3个有效数字, ≈1.732)
≈1.732)


[答案]13.9
17.(2010·浙江湖州)(本小题6分)计算:4+(-1)2010-tan45°.答案:解:原式=
 (2010·浙江湖州)5.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1:(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是(A)
(2010·浙江湖州)5.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1:(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是(A)
A.5米 B.10米 C.15米 D.10米
19.(2010·绵阳)(1)计算:(p-2010)0 +(sin60°)-1-︱tan30°- ︱+
︱+ .
.
答案:(1)原式= 1 + +
2 = 3 +
+
2 = 3 + =
3 +
=
3 + =
3.
=
3.
20.(莱芜)2009年首届中国国际航空体育节在莱芜雪野举办,
 期间在市政府广场进行了热气球飞行表演.如图,有一热气球到
期间在市政府广场进行了热气球飞行表演.如图,有一热气球到
达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B
的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应
至少再上升多少米?(结果精确到0.1米)
(参考数据:
 )
)
解:过A作AD⊥CB,垂足为点D. ………………………1分
 在Rt△ADC中,∵CD=36,∠CAD=60°.
在Rt△ADC中,∵CD=36,∠CAD=60°.
∴AD= ≈20.76.
……5分
≈20.76.
……5分
在Rt△ADB中,∵AD≈20.76,∠BAD=37°.
∴BD= ≈20.76×0.75=15.57≈15.6(米).
………8分
≈20.76×0.75=15.57≈15.6(米).
………8分
答:气球应至少再上升15.6米. …………………………9分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com