
2.掌握等可能事件的概率公式,并能熟练地运用排列组合的知识解决等可能事件的概率问题;
1.了解随机事件、必然事件、不可能事件的概念;
(四)巩固练习:
1.设 ,如果
,如果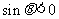 且
且 ,则
,则 的取值范围是(
的取值范围是(
 )
)


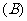





2.已知 的终边经过点
的终边经过点 ,且
,且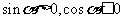 ,则
,则 的取值范围是
的取值范围是 .
.
3.若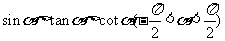 ,则
,则 (
( 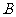 )
)


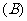





(三)例题分析:
例1.若 ,且
,且 , 则 (
, 则 (  )
)


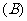





例2.(1)如果 是第一象限的角,那么
是第一象限的角,那么 是第几象限的角?
是第几象限的角?
(2)如果 是第二象限的角,判断
是第二象限的角,判断 的符号.
的符号.
解:(1)∵ ,
,
∴ ,
,
当 时,
时, ,
, 是第一象限的角,
是第一象限的角,
当 时,
时, ,
, 是第二象限的角,
是第二象限的角,
当 时,
时, ,
, 是第三象限的角.
是第三象限的角.
∴ 是第一,二,三象限的角.
是第一,二,三象限的角.
(2) 是第二象限的角,
是第二象限的角, ,
, ,
,
 ,
, ,∴
,∴ .
.
例3.(《高考 计划》考点24“智能训练第6题”) 已知锐角
计划》考点24“智能训练第6题”) 已知锐角 终边上的一点
终边上的一点 坐标是
坐标是 ,则
,则 (
(  )
)


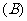


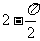


例4.扇形 的中心角为
的中心角为 ,半径为
,半径为 ,在扇形
,在扇形 中作内切圆
中作内切圆 及与圆
及与圆 外切,与
外切,与 相切的圆
相切的圆 ,问
,问 为何值时,圆
为何值时,圆 的面积最大?最大值是多少?
的面积最大?最大值是多少?
解:设圆 及与圆
及与圆 的半径分别为
的半径分别为 ,
,
则 ,得
,得 ,
,
∴ ,
,
∵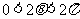 ,∴
,∴ ,令
,令 ,
,
 ,当
,当 ,即
,即 时,
时,
圆 的半径最大,圆
的半径最大,圆 的面积最大,最大面积为
的面积最大,最大面积为 .
.
(二)主要方法:
1.本节内容大多以选择、填空题形式出现,要重视一些特殊的解题方法,如数形结合法、代入检验法、特殊值法、待定系数法、排除法、另外还需掌握和运用一些基本结论.
(一)主要知识:
1.角的概念的推广;象限角、轴线角;与 角终边相同的角为
角终边相同的角为 ;
;
2.角的度量;角度制、弧度制及其换算关系;弧长公式 、扇形面积公式
、扇形面积公式 ;
;
3.任意角的三角函数.
2.掌握弧度制、弧度与角度的转化关系,扇形面积及弧长公式.
22、写作。
以“带着 ,一路前行”为题写一篇文章。
要求:
(1)根据自己所写内容(如理想、自信、尊严、感动、感恩、挫折、伤痛、遗憾、微笑、眼泪、鲜花等),补足题目,然后将完整的题目抄写在正文前;(2)诗歌除外,文体不限;(3)卷面整洁,字数600字左右;(4)文中不得出现真实的地名、校名、人名。
攀枝花市2010年高中阶段教育学校招生统一考试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com