
13.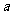 mol FeS与
mol FeS与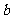 mol
mol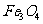 投入到
投入到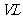 、
、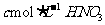 溶液(足量)中充分反应,产生NO气体,所得澄清溶液的成分可看作是
溶液(足量)中充分反应,产生NO气体,所得澄清溶液的成分可看作是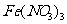 和
和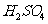 的混合溶液,反应中未被还原的硝酸为
的混合溶液,反应中未被还原的硝酸为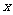 mol;若向反应后的混合液中加入
mol;若向反应后的混合液中加入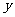 mol NaOH恰好使沉淀完全,则下列关系式正确的是
mol NaOH恰好使沉淀完全,则下列关系式正确的是
A.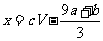 B.
B.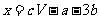
C.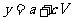 D.
D.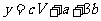
 第II卷(非选择题 共60分)
第II卷(非选择题 共60分)
12.在一容积固定的真空密闭容器中,投入1.5molX(g)和0.5molY(g),在一定温度下反应 达平衡,此时X的转化率为
达平衡,此时X的转化率为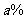 。若在同一温度同一容器中,最初投入的是3molX(g)和1molY(g),反应达到平衡时X的转化率为
。若在同一温度同一容器中,最初投入的是3molX(g)和1molY(g),反应达到平衡时X的转化率为 ,则下列判断正确的是
,则下列判断正确的是
A.若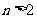 ,则
,则 B.若
B.若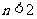 ,则
,则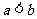
C.若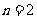 ,则
,则 D.若
D.若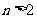 ,则
,则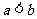
11.下列溶液中各微粒的物质的量浓度关系正确的

 是
是
A.向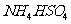 溶液中加入等物质的量的
溶液中加入等物质的量的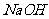 形成的溶液:
形成的溶液:
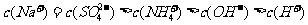
B.0.1mol/L的NaHS溶液中:
C.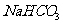 溶液中:
溶液中: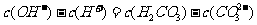
D.25℃时,将0.1mol/L 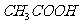 溶液滴入0.1mol/L
溶液滴入0.1mol/L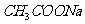 溶液中至pH=4:
溶液中至pH=4:
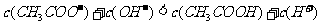
10.下列离子方程式正确的是
A.过氧化钠与水反应: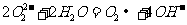
B.向碳酸氢镁溶液中加入过量的澄清石灰水:
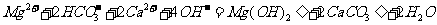
C.向明矾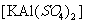 溶液中逐滴加入
溶液中逐滴加入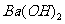 溶液至
溶液至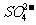 恰好完全沉淀:
恰好完全沉淀:
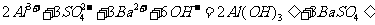
D.次氯酸钠与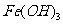 在碱性溶液中反应生成
在碱性溶液中反应生成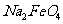 :
:
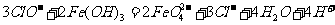
9.某有机物A的结构简式如右图所示,下列有关叙述正确的是
A.1mol A最多可以与2mol Br2发生反应
B.A在一定条件下可以发生消去反应和取代反应
C.一个A分子中最多有8个碳原子在同一平面上
D.1mol A与足量的NaOH溶液反应,最多可以消耗3mol NaOH
8.X、Y、Z、M是4种短周期元素,其中X、Y位于同一主族,Y与M、X与Z位于同一周期。X原子最外层电子数是其电子层数的3倍。Z原子的核外电子数比X原子少1。M是同周期中原子半径最大的元素(除稀有气体元素外)。下列说法正确的是
A.Z和X最多可以形成5种化合物
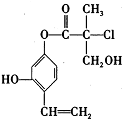 B.由X和Y组成的分子一定是非极性分子
B.由X和Y组成的分子一定是非极性分子
C.X、Y、Z元素的气态氢化物中,Y的沸点最高
D.四种元素简单离子的半径由大到小依次为Y>Z>X>M
7.下列事实能用同一原理解释的是
A.向硝酸银溶液和新制的Fe(OH)3胶体中分别加入少量稀盐酸均有沉淀产生
B.向氯化钡溶液中通入SO2气体后再加入氯水或氨水,都产生白色沉淀
C.向蛋白质溶液中加入饱和硫酸铵溶液或乙酸铅溶液,都产生白色沉淀
D.明矾和硫酸铁均可用于水的净化
6.“促进低碳经济,减少CO2的排放”是联合国《哥本哈根气候变化》会议的主题。下列措施中不符合这一主题的是
A.推广煤的干馏技术,提供清洁、高效的燃料
B.利用工业生产所产生的二氧化碳制造全降解塑料
C.限制化工发展,关停化工企业,消除污染源头
D.大力开发核能、太阳能、风能等新能源,以减少对化石能源的依赖
3、人造卫星中的“超重”、“失重”:
人造卫星中在发射阶段,尚未进入预定轨道的加速阶段,具有竖直向上的加速度,卫星内的所有物体处于超重状态,卫星与物体具有相同的加速度,由于高度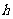 的增加,使
的增加,使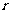 增加,导致
增加,导致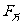 减小,同时由于升力的变化,使上升加速度
减小,同时由于升力的变化,使上升加速度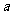 是个变量,设某一时刻即时加速度为
是个变量,设某一时刻即时加速度为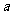 ,利用弹簧秤测量物体的重力的方法可间接求得距离地面的高度。
,利用弹簧秤测量物体的重力的方法可间接求得距离地面的高度。
例5、一物体在地球表面重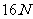 ,它在以
,它在以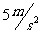 的加速度上升的火箭中的视重为
的加速度上升的火箭中的视重为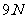 ,
,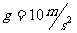 ,则此时火箭离地面的距离为地球半径的多少倍?
,则此时火箭离地面的距离为地球半径的多少倍?
解析:以物体为对象分析如图所示,设距离地面高度为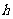 ,则:
,则: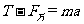
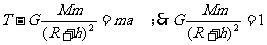
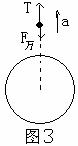 近地附近:
近地附近: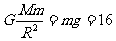 ;联立两式解得:
;联立两式解得: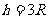
卫星进入正常运行轨道,由相同的间距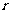 决定各物体具有相同的运动状态
决定各物体具有相同的运动状态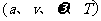 。卫星上的所有物体为什么处于完全失重状态,这是理解的一个难点,减小学生理解难的方法就是采用反证法:假设卫星上所有物体还受到其它力的作用,则:
。卫星上的所有物体为什么处于完全失重状态,这是理解的一个难点,减小学生理解难的方法就是采用反证法:假设卫星上所有物体还受到其它力的作用,则:
 ,
,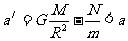 ,假设不成立,因此,凡一切工作原理涉及到重力的有关仪器在卫星中都不能正常使用。
,假设不成立,因此,凡一切工作原理涉及到重力的有关仪器在卫星中都不能正常使用。

2、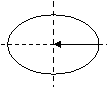 万有引力、向心力和重力
万有引力、向心力和重力
对于赤道上的某一个物体
,有  当速度增加时,重力减小,向心力增加,当速度
当速度增加时,重力减小,向心力增加,当速度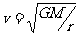 (即第一宇宙速度)时,mg = 0,物体将“飘”起来,星球处于瓦解的临界状态。
(即第一宇宙速度)时,mg = 0,物体将“飘”起来,星球处于瓦解的临界状态。
例6、某星球壳视为球体,自转周期为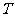 ,在它的两极处,用弹簧秤测得物体重为
,在它的两极处,用弹簧秤测得物体重为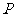 ,在它的赤道上,用弹簧秤测得同一物体重为
,在它的赤道上,用弹簧秤测得同一物体重为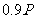 ,求星球的平均密度?
,求星球的平均密度?
解析:设星球的半径为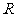 ,在两极和赤道上的重力及速度分别为
,在两极和赤道上的重力及速度分别为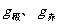
两极: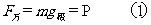
赤道上: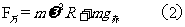
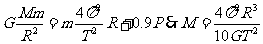
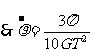
例7、如果地球自转速度加快,地球上物体的重量将发生怎样的变化?地球自转角速度等于多少时,在赤道上物体的重量为零?这时一昼夜将有多长?
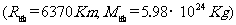
解析:以赤道上的物体为研究对象,设转速为
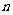 ,则:
,则:

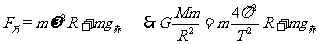 ;
;

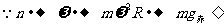 ;设地球自转的角速度为
;设地球自转的角速度为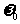 时,
时,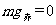 ,则:
,则:


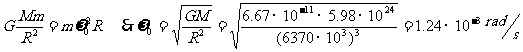


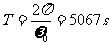
例8 、已知物体从地球上的逃逸速度(第二宇宙速度)v=√2GME/RE,其中G、ME、RE分别是万有引力恒量、地球的质量和半径.已知G=6.67×10-11N·m2/kg2,c=2.9979×108m/s.求下列问题:
(1)逃逸速度大于真空中光速的天体叫做黑洞.设某黑洞的质量等于太阳的质量M=1.98×1030kg,求它的可能最大半径(这个半径叫Schwarz-Child半径);
(2)在目前天文观测范围内,物质的平均密度为10-27kg/m3,如果认为我们的宇宙是这样一个均匀大球体,其密度使得它的逃逸速度大于光在真空中的速度c,因此任何物体都不能脱离宇宙,问宇宙的半径至少多大?
解:(1)由题目所提供的信息可知,任何天体均存在其所对应的逃逸速度v=√2GM/R,其中M、R为天体的质量和半径.
对于黑洞模型来说,其逃逸速度大于真空中的光速,即v>c,也就是√2GM/R>c.
黑洞半径 R<2GM/c2=2939m=2.94km.
即质量为1.98×1030kg的黑洞的最大半径为2.94km.
(2)把宇宙视为一普通天体,则质量为 M=ρ·V=ρ·4πR3/3 ①其中R为宇宙半径,ρ为宇宙的密度,则宇宙所对应的逃逸速度 v=√2GM/R ②
由于题设中宇宙密度使得其逃逸速度大于真空中光速c,即v>c. ③则由上述①②③式可解得宇宙半径R>√3c2/8πρG=4×1026m.
因1光年=365×24×3600×2.9979×108m,所以R>4.23×1010光年.
即宇宙半径至少为4.23×1010光年.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com