
9.100名学生分四个兴趣小组参加物理、化学、数学、计算机竞赛辅导,人数别是30、27、23、20.
(1)列出学生参加兴趣小组的频率分布表;
(2)画出表示频率分布的条形图.
8.有一个容量为100的样本,数据的分组及各组的频数如下:
|
区间 |
[12,15) |
[15,18) |
[18,21) |
[21,24) |
[24,27) |
[27,30) |
[30,133) |
|
频数 |
6 |
16 |
18 |
22 |
20 |
10 |
8 |
(1)列出样本的频率分布表;(2)画出频率分布直方图;(3)估计数据小于30的概率.
7.为了比较甲、乙两位划艇运动员的成绩,在相同的条件下对他们进行了6次测验,测得他们的平均速度(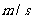 )分别如下:
)分别如下:
甲:2.7 3.8 3.0 3.7 3.5 3.1
乙:2.9 3.9 3.8 3.4 3.6 2.8
试根据以上数据,判断他们谁更优秀.
6.有一组数据: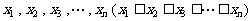 ,它们的算术平均值为10,若去掉其中最大的
,它们的算术平均值为10,若去掉其中最大的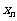 ,余下数据的算术平均值为9;若去掉其中最小的
,余下数据的算术平均值为9;若去掉其中最小的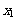 ,余下数据的算术平均值为11,则
,余下数据的算术平均值为11,则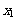 关于n的表达式为
;
关于n的表达式为
;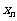 关于
关于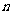 的表达式为
.
的表达式为
.
5.某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2:3:5.现用分层抽样方法抽出一个容量为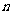 的样本,样本中A种型号产品有16件,那么此样本的容量
的样本,样本中A种型号产品有16件,那么此样本的容量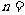 .
.
4.一个总体的个数为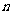 ,用简单随机抽样的方法,抽取一个容量为
,用简单随机抽样的方法,抽取一个容量为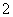 的样本,个体
的样本,个体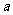 第一次未被抽到,个体
第一次未被抽到,个体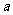 第一次未被抽到第二次被抽到,以及整个过程中个体
第一次未被抽到第二次被抽到,以及整个过程中个体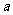 被抽到的概率分别是
.
被抽到的概率分别是
.
3.在抽查某产品的尺寸过程中,将其尺寸分成若干组, 是其中一组,抽查出的个体数在该组上的频率为
是其中一组,抽查出的个体数在该组上的频率为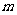 ,该组上的直方图的高为
,该组上的直方图的高为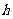 ,则
,则 等于
(
)
等于
(
)
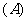
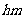

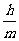
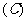
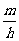
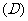 与
与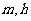 无关
无关
2.欲对某商场作一简要审计,通过检查发票及销售记录的2%来快速估计每月的销售总额.现采用如下方法:从某本50张的发票存根中随机抽一张,如15号,然后按序往后将65号,115号,165号,…发票上的销售额组成一个调查样本.这种抽取样本的方法是 ( )
 简单随机抽样
简单随机抽样  系统抽样
系统抽样  分层抽样
分层抽样  其它方式的抽样
其它方式的抽样
1.一个单位有职工160人,其中业务人员96人,管理人员40人,后勤人员24人,为了解职工身体情况,要从中抽取一个容量为20的样本,如用分层抽样,则管理人员应抽到多少个 ( )

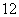
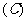
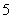
例1.某中学有员工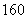 人,其中中高级教师
人,其中中高级教师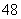 人,一般教师
人,一般教师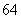 人,管理人员
人,管理人员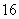 人,行政人员
人,行政人员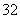 人,从中抽取容量为
人,从中抽取容量为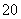 的一个样本.以此例说明,无论使用三种常用的抽样方法中的哪一种方法,总体中的每个个体抽到的概率都相同.
的一个样本.以此例说明,无论使用三种常用的抽样方法中的哪一种方法,总体中的每个个体抽到的概率都相同.
解:(1)(简单随机抽样)可采用抽签法,将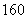 人从
人从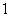 到
到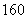 编号,然后从中抽取
编号,然后从中抽取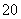 个签,与签号相同的
个签,与签号相同的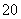 个人被选出.显然每个个体抽到的概率为
个人被选出.显然每个个体抽到的概率为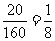 .
.
(2)(系统抽样法)将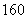 人从
人从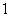 到
到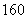 编号,,按编号顺序分成
编号,,按编号顺序分成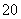 组,每组
组,每组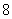 人,先在第一组中用抽签法抽出
人,先在第一组中用抽签法抽出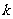 号(
号(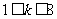 ),其余组的
),其余组的
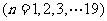 也被抽到,显然每个个体抽到的概率为
也被抽到,显然每个个体抽到的概率为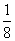 .
.
(3)(分层抽样法)四类人员的人数比为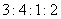 ,又
,又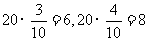
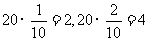 ,所以从中高级教师、一般教师、管理人员、行政人员中分别抽取
,所以从中高级教师、一般教师、管理人员、行政人员中分别抽取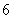 人、
人、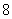 人、
人、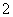 人、
人、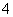 人,每个个体抽到的概率为
人,每个个体抽到的概率为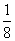 .
.
例2.质检部门对甲、乙两种日光灯的使用时间进行了破坏性试验,10次试验得到的两种日光灯的使用时间如下表所示,问:哪一种质量相对好一些?
|
|
解:甲的平均使用寿命为:
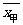
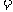
 =2121(h),
=2121(h),
甲的平均使用寿命为 :
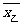 =
=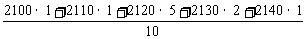 =2121(h),
=2121(h),
甲的方差为: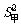 =
=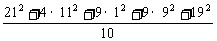 =129(h2),
=129(h2),
乙的方差为: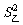 =
=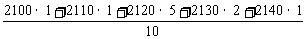 =109(h2),
=109(h2),
∵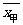 =
=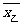 ,且
,且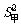 >
>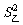 ,∴乙的质量好一些.
,∴乙的质量好一些.
例3.下表给出了某学校120名12岁男生的身高统计分组与频数(单位:cm).
|
区间 |
[122,126) |
[126,130) |
[130,134) |
[134,138) |
[138,142) |
[142,146) |
[146,150) |
[150,154) |
[154,158) |
|
人数 |
5 |
8 |
10 |
22 |
33 |
20 |
11 |
6 |
5 |
(1)列出样本的频率分布表(含累积频率);
(2)画出频率分布直方图;
(3)根据累积频率分布,估计小于134的数据约占多少百分比.
解:(1)样本的频率分布表与累积频率表如下:
|
区间 |
[122,126) |
[126,130) |
[130,134) |
[134,138) |
[138,142) |
[142,146) |
[146,150) |
[150,154) |
[154,158) |
|
人数 |
5 |
8 |
10 |
22 |
33 |
20 |
11 |
6 |
5 |
|
频率 |
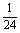 |
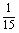 |
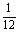 |
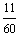 |
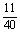 |
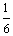 |
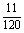 |
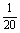 |
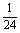 |
|
累积频率 |
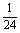 |
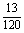 |
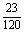 |
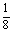 |
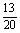 |
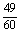 |
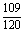 |
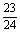 |
1 |
(2)频率分布直方图如下:
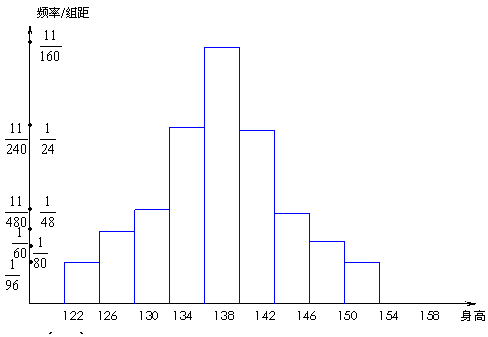
(3)根据累积频率分布,小于134的数据约占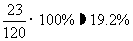 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com