
3.在等比数列{an}中,a1>1,且前n项和Sn满足 ,那么a1的取值范围是( )(98年)
,那么a1的取值范围是( )(98年)
(A)(1,+∞) (B)(1,4) (C)(1,2) (D)(1, )
)
2.
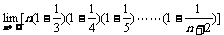 的值等于( )(91年)
的值等于( )(91年)
(A)0 (B)1 (C)2 (D)3
例1.用数学归纳法证明2n>n2 (n∈N,n³5),则第一步应验证n= ;
例2.用数学归纳法证明 ,第一步验证不等式 成立;
,第一步验证不等式 成立;
例3.是否存在常数a,b,c,使得等式1·22+2·32+……+n(n+1)2= (an2+bn+c)对一切自然数n成立?并证明你的结论.(89年)
(an2+bn+c)对一切自然数n成立?并证明你的结论.(89年)
例4.已知数列{an}= ,记Sn=a1+a2+a3+…+an,用数学归纳法证明Sn=(n+1)an-n.
,记Sn=a1+a2+a3+…+an,用数学归纳法证明Sn=(n+1)an-n.
例5.证明: >
> (n∈N,n³2)
(n∈N,n³2)
例6.证明:xn─nan─1x+(n─1)an能被(x─a)2整除(a≠0).
例7.在1与2之间插入 个正数
个正数 ,使这
,使这 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入 个正数
个正数 使这
使这 个数成等差数列.记
个数成等差数列.记 .
.
(Ⅰ)求数列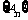 和
和 的通项;(Ⅱ)当
的通项;(Ⅱ)当 时,比较
时,比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
例8.若数列{an}满足对任意的n有:Sn= ,试问该数列是怎样的数列?并证明你的结论.
,试问该数列是怎样的数列?并证明你的结论.
例9.已知数列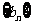 是等差数列,
是等差数列,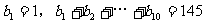 。
。
(Ⅰ)求数列 的通项
的通项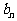 ;(Ⅱ)设数列
;(Ⅱ)设数列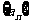 的通项
的通项 (其中
(其中 ,且
,且 ),记
),记 是数列
是数列 的前n项和。试比较
的前n项和。试比较 与
与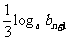 的大小,并证明你的结论。
的大小,并证明你的结论。
练习(数列的极限)
1.
已知{an}是等比数列,如果a1+a2+a3=18,a2+a3+a4=-9,Sn=a1+a2+……+an,那么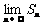 的值等于( )(89年)
的值等于( )(89年)
(A)8 (B)16 (C)32 (D)48
例1.(1)
 =
;
=
;
2).数列{an}和{bn}都是公差不为0的等差数列,且 =3,则
=3,则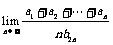 =
=
3.)
 (a>1)=
;
(a>1)=
;
(4). =
;
=
;
(5). =
;
=
;
(6).等比数列{an}的公比为q=─1/3,则 = ;
= ;
例2.将无限循环小数 ;1.32
;1.32
 化为分数.
化为分数.
例3.已知 ,求实数a,b的值;
,求实数a,b的值;
例4.数列{an},{bn}满足 (2an+bn)=1,
(2an+bn)=1,  (an─2bn)=1,试判断数列{an},{bn}的极限是否存在,说明理由并求
(an─2bn)=1,试判断数列{an},{bn}的极限是否存在,说明理由并求 (anbn)的值.
(anbn)的值.
例5.设首项为a,公差为d的等差数列前n项的和为An ,又首项为a,公比为r的等比数列前n项和为Gn
,其中a≠0,|r|<1.令Sn=G1+G2+…+Gn,若有 =a,求r的值.
=a,求r的值.
例6.设首项为1,公比为q(q>0)的等比数列的前n项之和为Sn,又设Tn= ,求
,求 .
.
例7.{an}的相邻两项an,an+1是方程x2─cnx+ =0的两根,又a1=2,求无穷等比c1,c2,…cn, …的各项和.
=0的两根,又a1=2,求无穷等比c1,c2,…cn, …的各项和.
例8.在半径为R的圆内作内接正方形,在这个正方形内作内切圆,又在圆内作内接正方形,如此无限次地作下去,试分别求所有圆的面积总和与所有正方形的面积总和。
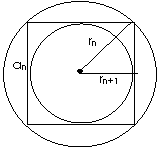
例9.如图,B1,B2,…,Bn,…顺次为曲线y=1/x(x>0)上的点,A1,A2,…,An…顺次为ox轴上的点,且三角形OB1A1,三角形A1B2A2,三角形An─1BnAn为等腰三角形(其中Ð Bn为直角),如果An的坐标为(xn,0).
(1)求出An的横坐标的表达式;
 (2)求
(2)求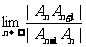 .
.
破釜沉舟!!攻克语音关!(14)
|
240 |
拘泥 |
|
250 |
泡桐 |
|
|
241 |
拙劣 |
|
251 |
泥古 |
|
|
242 |
择菜 |
|
252 |
泥泞 |
|
|
243 |
昂扬 |
|
253 |
泥淖 |
|
|
244 |
杳然 |
|
254 |
泫然流涕 |
|
|
245 |
枞树 |
|
255 |
泯灭 |
|
|
246 |
氛围 |
|
256 |
浅濑 |
|
|
247 |
沮丧 |
|
257 |
狙击 |
|
|
248 |
油坊 |
|
258 |
疟疾 |
|
|
249 |
沼气 |
|
259 |
空城计 |
|
5. 请筛选整合下面文字中的主要意思,提炼出关于“碳中和”定义的4个关键词语。(4分)
“碳中和”的目的是为了环保。人们计算自己日常活动制造的二氧化碳排放量,包括直接的和间接的,并计算抵消这些二氧化碳所需的经济成本。人们可以通过植树或其他环保项目吸收大气中相应的二氧化碳;个人也可以付款给专门企业或机构,由这些企业或机构通过植树或其他环保项目吸收大气中相应的二氧化碳。2006年,《新牛津美国字典》将“碳中和”评为当年年度词汇。它已经从最初由环保人士倡导的一项概念,逐渐获得越来越多民众支持,并且成为受到许多国家政府当局所重视的实际绿化行动。
3.下列各句中,没有语病的一句是
A.我国税务机关正在加紧完善涉外税收征管体系,以更好地适应美国次级贷款
危机所带来的涉外贸易新变化。
B.随着世博会开幕日期的临近,“世博”已经成了使用频率最高的上海市民口头
语,可见人们纷纷以不同方式关注世博。
C.各位观众,今天是二十四节气中的小寒,它代表今天是入冬以来最寒冷的季
节,请注意添加衣服,预防感冒。
D.2009年央视春晚总导演建议,在四川和台北设立分会场,将五大洲各华语媒
体的祝福传送过来,营造全球华人喜庆祥和大联欢。
2.下列各句中,加点的成语使用恰当的一句是
A.去年春节,我国大部分地区风云变幻,有的晴空丽日,有的雨雪交加,恶劣
的天气给人们的生活带来了不少麻烦。
B.《谍影重重3》所创造的完美境界,彻底颠覆了传统的间谍电影,不少影迷对
伯恩顶礼膜拜,认为伯恩的表演比邦德更胜一筹。
C.建设环境友好型社会不单是政府的事情,环保与人类生活休戚相关,善待大自
然是每一个地球人的义务和责任。
D.生活中并不存在真正的完美,只要我们在做每一件事情时,都全神贯注,做得
入木三分,对自己来说就已经是完美之极了。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com