
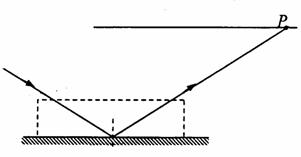
15.(10分)如图所示,一束光线以60°的入射角射到一水平放置的平面镜上,反射后在正上方与平面镜平行的光屏上留下一光点P。现将一块上下两面平行的透明体平放在平面镜上,
如图中虚线所示,则进入透明体的光线经平面镜反射后再从透明体的上表面射出,打在光屏上的光点P′与原来相比向左平移了3.46cm,已知透明体对光的折射率为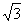 。
。
(1)作出后来的光路示意图,标出P′位置;
(2)透明体的厚度为多大?
(3)光在透明体里运动的时间多长?(结果保留两位有效数字)
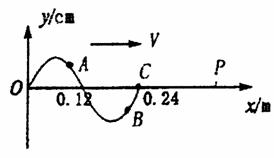
14.(10分)一列向右传播的简谐横波,某时刻的波形如图所示,波速为0.6m/s,P点的横坐标x=0.96m,从图示时刻开始计时,此时波刚好传到C点。
(1)此时刻质点A的运动方向和质点B的加速度方向是怎样的?
(2)经过多少时间P点第二次达到波峰?
(3)画出P质点开始振动后的振动图象。
13.(8分)跳伞运动员476米高空自由下落,下落一段时间后才打开伞,开伞后以2m/s2的加速度匀减速竖直下落,到达地面的速度为4m/s(g取10m/s2),求运动员在空中下落的时间和自由下落的距离?
12.(12分)在“探究加速度与力、质量的关系”的实验时,我们已经知道,物体的加速度(a)同时跟合外力(F)和质量(m)两个因素有关。要研究这三个物理量之间的定量关系的基本思路是:先保持m不变,研究a与F的关系,再保持F不变,研究a与m的关系。
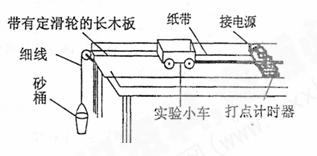
(1)小薇同学的实验方案如图所示,她想用砂和砂桶的重力表示小车受到的合外力,为了减少这种做法而带来的实验误差,你认为在实验中还应该采取的两项措施是:
a.
b.
(2)小薇同学利用实验中打出的纸带求加速度时,处理方案有两种,a.利用公式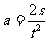 计算;根据
计算;根据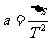 利用逐差法计算。两种方案中,你认为选择方案 比较合理,而另 一种方案不合理的理由是
。
利用逐差法计算。两种方案中,你认为选择方案 比较合理,而另 一种方案不合理的理由是
。
(3)下表是小薇同学在探究“保持m不变,a与F的关系”时记录的一组实验数据,请你根据表格中的数据在下面的坐标中做出a-F图像:
|
物理量 次数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
m砂(㎏) |
0.010 |
0.020 |
0.030 |
0.040 |
0.050 |
0.060 |
|
(N) |
0.098 |
0.196 |
0.294 |
0.392 |
0.490 |
0.588 |
|
a(m/s2) |
0.196 |
0.390 |
0.718 |
0.784 |
0.990 |
1.176 |
(4)针对小薇同学的实验设计、实验操作、数据采集与处理,就其中的某一环节,提出一条你有别于小薇同学的设计或处理方法: 。

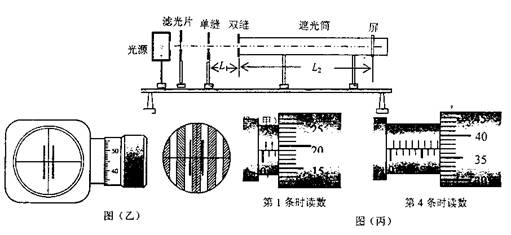
11.(8分)用双缝干涉测光的波长。实验装置如图(甲)所示,已知单缝与双缝间的距离L1=100㎜,双缝与屏的距离L2=700㎜,双缝间距d=0.25㎜。用测量头来测量亮纹中心的距离。测量头由分划板、目镜、手轮等构成,转动手轮,使分划板左右移动,让分划板的中心刻线对准亮纹的中心(如图(乙)所示),记下此时手轮上的读数,转动测量头,使分划板中心刻线对准另一条亮纹的中心,记下此时手轮上的读数。
(1)分划板的中心刻线分别对准第1条和第4第条亮纹的中心时,手轮上的读数如图(丙)所示,,则对准第1条时读数X1= ㎜、对准第4条时读数X2= ㎜。
 (2)写出计算波长
(2)写出计算波长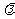 的表达式,
的表达式,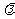 =
(用符号表示),
=
(用符号表示),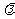 = nm。
= nm。
19.解析:设球的内接圆柱的底半径为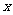 ,则其高为
,则其高为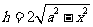 ,所以圆柱的体积是
,所以圆柱的体积是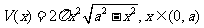 ,
,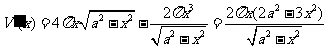
 (2)由(1)中的分析可以猜想
(2)由(1)中的分析可以猜想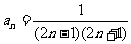 。下面用数学归纳法证明:
。下面用数学归纳法证明:
①当n=1时,公式显然成立。②假设当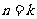 时成立,即
时成立,即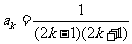 ,那么由已知,得
,那么由已知,得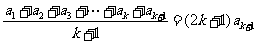 ,
,
即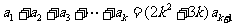 所以
所以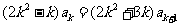
即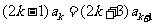 ,又归纳假设,得:
,又归纳假设,得: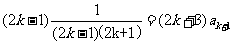
所以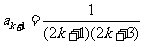 ,即当
,即当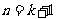 时,公式也成立
时,公式也成立
由①,②,对一切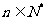 ,都有
,都有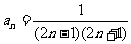 成立。
成立。
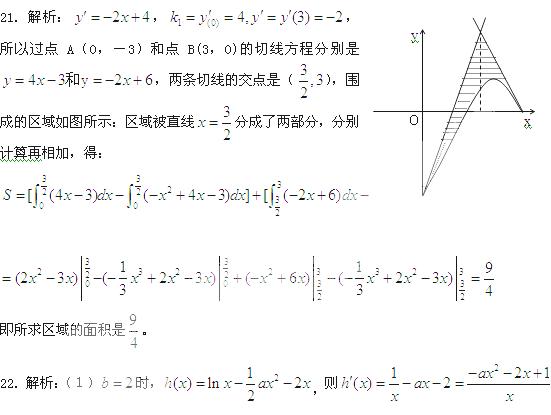 因为函数
因为函数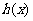 存在单调递减区间,所以
存在单调递减区间,所以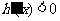 有解,即
有解,即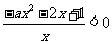 ,又因为
,又因为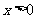 ,
,
则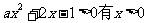 的解。①当
的解。①当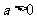 时,
时,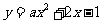 为开口向上的抛物线,
为开口向上的抛物线,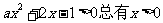 的解;②当
的解;②当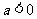 时,
时,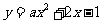 为开口向下的抛物线,
为开口向下的抛物线,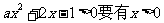 的解,所以
的解,所以 ,且方程
,且方程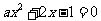 至少有一个正根,所以
至少有一个正根,所以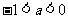 。综上可知,
。综上可知,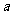 得取值范围是
得取值范围是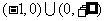 。
。
(2)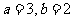 时,
时, ,
,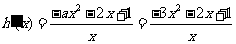 ,
,
令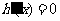 ,则
,则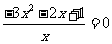 ,所以
,所以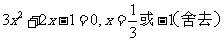
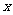 |
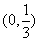 |
 |
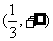 |
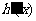 |
+ |
0 |
- |
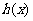 |
 |
极大值 |
 |
列表:
所以当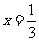 时,
时,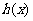 取的最大值
取的最大值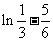
又当 时,
时,
所以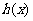 的取值范围是
的取值范围是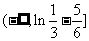 。
。
18. 解析:(1)
解析:(1)
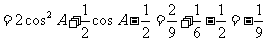
(2)由余弦定理得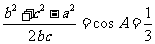 ,所以
,所以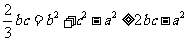
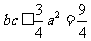 ,当且仅当
,当且仅当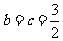 时,等号成立,即
时,等号成立,即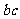 的最大值为
的最大值为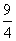 。
。
13.解析: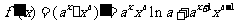 ,故填
,故填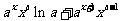 ;
;
12.解析:当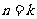 时,左端=
时,左端=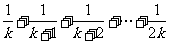 ;
;
当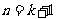 时,左端=
时,左端= 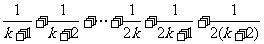 显然选C
显然选C
11.解析:(1)两个实数可以比较大小,(2)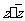 为实数,
为实数,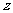 可以为纯虚数;(3)原点,(4)正确,
故选A
可以为纯虚数;(3)原点,(4)正确,
故选A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com