
3.在波的传播方向上,距离一定的P与Q点之间只有一个波谷的四种情况,如图A、B、C、D所示。已知这四列波在同一种介质中均向右传播,则质点P能首先达到波谷的是( )

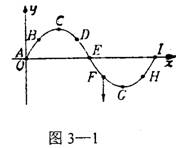 1.一简谐横波在x轴上传播,在某时刻的波形如图3-1所示。已知此时质点F的运动方向向下,则 ( )
1.一简谐横波在x轴上传播,在某时刻的波形如图3-1所示。已知此时质点F的运动方向向下,则 ( )
A.此波沿x轴负方向传播
B.质点D此时向下运动
C.质点B将比质点C先回到平衡位置
 D.质点E振幅为零
D.质点E振幅为零
2.劲度系数为20N/cm的弹簧振子,它的振动图
象如图所示,在图中A点对应的时刻( )
A.振子所受的弹力大小为5N,方向指向x轴
的负方向
B.振子的速度方向指向x轴的正方向
C.在0-4s内振子作了1.75次全振动
D.在0-4s内振子通过的路程为0.35cm,位移为0
21.(本小题满分12分)
解:(Ⅰ)∵ 有两个不等正根,
有两个不等正根,
即方程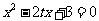 有两个不等正根
有两个不等正根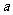 、
、 …………………………………1分
…………………………………1分
∴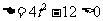 且
且 ,
,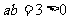 ………………………………2分
………………………………2分
解得: …………………………………………………………3分
…………………………………………………………3分
(Ⅱ) ……………………………4分
……………………………4分
令 ,则
,则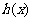 的对称轴为
的对称轴为
∴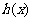 在
在 上的最小值为
上的最小值为
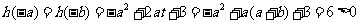 ………………………5分
………………………5分
∴ ……………………………………………………………6分
……………………………………………………………6分
于是 在
在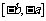 上单调递增。 ………………………………7分
上单调递增。 ………………………………7分
(Ⅲ)由(Ⅱ)可知: 在
在 上单调递增
上单调递增
∴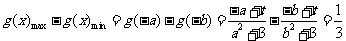 ………………………8分
………………………8分
即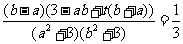
又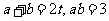 ,
,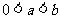
解得: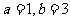 ……………………………………………………9分
……………………………………………………9分
∴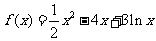 ,∴
,∴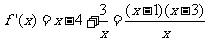 ,
,
∴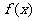 在
在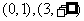 上递增,在
上递增,在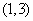 上递减且当
上递减且当 时,
时,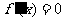
∴ ,
, ………………10分
………………10分
又当 时,
时, ;当
;当 时,
时,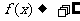 …………………11分
…………………11分
∴当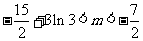 时,方程
时,方程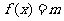 有3个不同的解
有3个不同的解
∴实数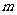 的取值范围为
的取值范围为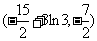 。
…………………………12分
。
…………………………12分
20.(本小题满分12分)
 (Ⅰ)证明:由四边形
(Ⅰ)证明:由四边形 为菱形,
为菱形,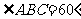 ,
,
可得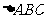 为正三角形。因为
为正三角形。因为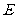 为
为 的中点,所以
的中点,所以 。 …………1分
。 …………1分
又 ∥
∥ ,因此
,因此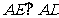 。…………………………………………………2分
。…………………………………………………2分
因为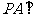 平面
平面 ,
,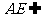 平面
平面 ,所以
,所以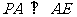 。 ………3分
。 ………3分
而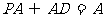 ,所以
,所以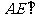 平面
平面 。 ………………………………4分
。 ………………………………4分
又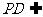 平面
平面 ,所以
,所以 。 ……………………………………5分
。 ……………………………………5分
(Ⅱ)解:设 ,
,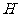 为
为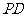 上任意一点,连接
上任意一点,连接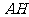 、
、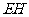
由(Ⅰ)可知: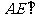 平面
平面 ,
,
则 为
为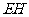 与平面
与平面 所成的角。……………………………………………6分
所成的角。……………………………………………6分
在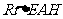 中,
中, ,
,
所以当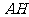 最短时,
最短时, 最大, ………………………………………………7分
最大, ………………………………………………7分
即当 时,
时, 最大,此时
最大,此时 。
。
因此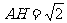 。又
。又 ,所以
,所以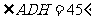 ,于是
,于是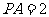 。 ……………………8分
。 ……………………8分
因为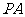 ⊥平面
⊥平面 ,
,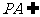 平面
平面 ,
,
所以平面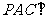 平面
平面 。 …………………………………………9分
。 …………………………………………9分
过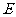 作
作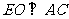 于
于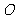 ,则由面面垂直的性质定理可知:
,则由面面垂直的性质定理可知: 平面
平面 ,
,
过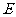 作
作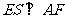 于
于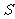 ,连接
,连接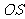 ,
,
则由三垂线定理可知: 为二面角
为二面角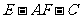 的平面角。 ……………………10分
的平面角。 ……………………10分
在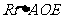 中,
中,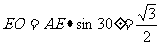 ,
,
又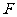 是
是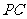 的中点,在
的中点,在 中,
中,
又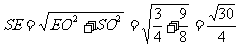 ………………………………11分
………………………………11分
在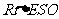 中,
中,
即二面角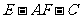 的余弦值为
的余弦值为 。 ………………………………12分
。 ………………………………12分
19.(本小题满分12分)
解:(Ⅰ)由题意可知,甲喊一次就获胜的概率为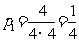 。…………………5分
。…………………5分
(Ⅱ)喊一次:甲胜的概率为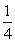 …………………………………………6分
…………………………………………6分
甲乙不分胜负的概率为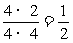 …………………………8分
…………………………8分
甲负的概率为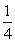 ……………………………………………9分
……………………………………………9分
∴甲在喊不超过三次的情况下就获胜的概率为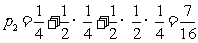 。 ………12分
。 ………12分
18.(本小题满分13分)
解:(Ⅰ)∵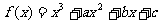 ∴
∴ ………………1分
………………1分
又函数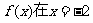 处取得极值 ∴
处取得极值 ∴ ①………………3分
①………………3分
又函数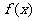 的图象与直线
的图象与直线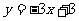 在点(1,0)处相切
在点(1,0)处相切
∴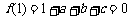 ②
………………………………………………………4分
②
………………………………………………………4分
 ③
………………………………………………………………6分
③
………………………………………………………………6分
由①②③解得: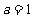 ,
, ,
,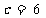 。……………………………………………7分
。……………………………………………7分
(Ⅱ)由(Ⅰ)可得: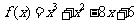 ,
, ……8分
……8分
当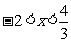 时,
时, ,函数
,函数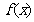 的单调递减区间为
的单调递减区间为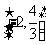 ; …………………10分
; …………………10分
当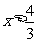 或
或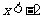 时,
时, ,函数
,函数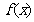 的单调递增区间为
的单调递增区间为 ,
, 。…13分
。…13分
17.(本小题满分13分)
解:(Ⅰ)令 ,则
,则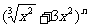 展开式的各项系数和为
展开式的各项系数和为 ………………………………3分
………………………………3分
又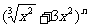 展开式的各项二项式系数和为
展开式的各项二项式系数和为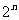 ……………………………………………5分
……………………………………………5分
∴ 即
即 ………………………………………………………………6分
………………………………………………………………6分
于是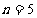 ……………………………………………………………………………………7分
……………………………………………………………………………………7分
(Ⅱ)由(Ⅰ)可知: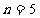 ∴
∴ 展开式的中间两项二项式系数最大………9分
展开式的中间两项二项式系数最大………9分
即 ……………………………………………11分
……………………………………………11分
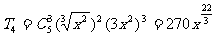 。 ………………………………………13分
。 ………………………………………13分
16.(本小题满分13分)
 (Ⅰ)证明:连结
(Ⅰ)证明:连结 ,令
,令 ,则
,则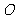 为
为 的中点………1分
的中点………1分
而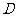 为
为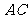 的中点 ∴
的中点 ∴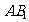 ∥
∥ ………………………………………………3分
………………………………………………3分
又 ,
,
∴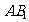 ∥平面
∥平面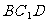 ………………………………………………………………6分
………………………………………………………………6分
(Ⅱ)解:由(Ⅰ)可知: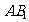 ∥
∥
∴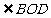 (或其补角)为异面直线
(或其补角)为异面直线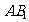 与
与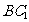 所成的角 …………………………………………………8分
所成的角 …………………………………………………8分
又正三棱柱 的所有棱长都为2,
的所有棱长都为2,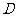 为
为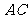 的中点
的中点
∴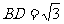 ,
, ,
, ,
,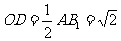 …………………………9分
…………………………9分
在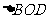 中,
中, …………………………………11分
…………………………………11分
∴异面直线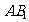 与
与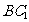 所成的角为
所成的角为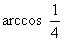 。 ……………………………………………………………13分
。 ……………………………………………………………13分
11. 12.
12.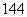 13.
13. 14.
14.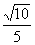 15.
15. ,
,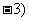
21.(本小题满分12分)已知函数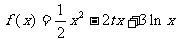 ,
, ,函数
,函数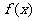
在 、
、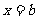 处取得极值,其中
处取得极值,其中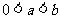 。
。
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)判断 在
在 上的单调性;
上的单调性;
(Ⅲ)已知 在
在 上的最大值比最小值大
上的最大值比最小值大
 ,若方程
,若方程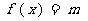 有3个不同的解,
有3个不同的解,
求实数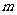 的取值范围。
的取值范围。
参考解答及评分意见
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com