
3.已知下列命题中:
(1)若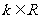 ,且
,且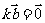 ,则
,则 或
或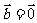 ,
,
(2)若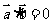 ,则
,则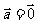 或
或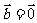
(3)若不平行的两个非零向量 ,满足
,满足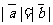 ,则
,则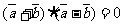
(4)若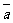 与
与 平行,则
平行,则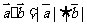 其中真命题的个数是( )
其中真命题的个数是( )
A.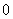 B.
B. C.
C. D.
D.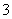
2.设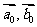 分别是与
分别是与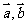 向的单位向量,则下列结论中正确的是( )
向的单位向量,则下列结论中正确的是( )
A.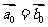 B.
B.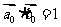
C.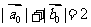 D.
D.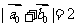
1.化简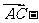
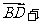
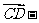
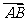 得( )
得( )
A. B.
B.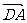 C.
C.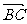 D.
D.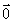
5.在求几个函数的和(或积)的极限时,一般要化简,再求极限.
六 作业(求下列极限)
(1)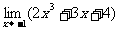 (2)
(2)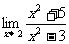 (3)
(3)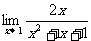
(4)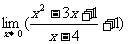 (5)
(5)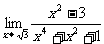 (6)
(6)
(7)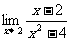 (8)
(8)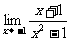 (9)
(9)
(10)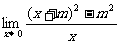 (11)
(11)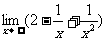 (12)
(12)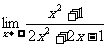
(13) (14)
(14)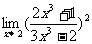 (15)
(15)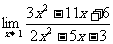
(16) (17)
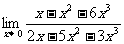
(17)
(18)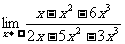
4.两个(或几个)函数的极限至少有一个不存在时,他们的和、差、积、商的极限不一定不存在.
3.函数的运算法则成立的前提条件是函数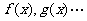 的极限存在,在进行极限运算时,要特别注意这一点.
的极限存在,在进行极限运算时,要特别注意这一点.
2.有限个函数的和(或积)的极限等于这些函数的和(或积);
 如果
如果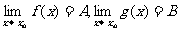 ,那么
,那么

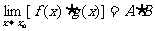
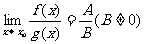
也就是说,如果两个函数都有极限,那么这两个函数的和、差、积、商组成的函数极限,分别等于这两个函数的极限的和、差、积、商(作为除数的函数的极限不能为0).
说明:当C是常数,n是正整数时,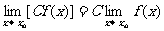
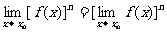
这些法则对于 的情况仍然适用.
的情况仍然适用.
三 典例剖析
例1.求下列函数在X=0处的极限
(1)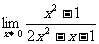 (2)
(2)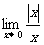 (3)
(3)
例2 求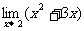
例3 求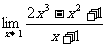
例4 求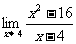
分析:当 时,分母的极限是0,不能直接运用上面的极限运用法则.注意函数
时,分母的极限是0,不能直接运用上面的极限运用法则.注意函数 在定义域
在定义域 内,可以将分子、分母约去公因式
内,可以将分子、分母约去公因式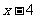 后变成
后变成 ,由此即可求出函数的极限.
,由此即可求出函数的极限.
例5 求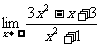
分析:当 时,分子、分母都没有极限,不能直接运用上面的商的极限运算法则.如果分子、分母都除以
时,分子、分母都没有极限,不能直接运用上面的商的极限运算法则.如果分子、分母都除以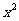 ,所得到的分子、分母都有极限,就可以用商的极限运用法则计算。
,所得到的分子、分母都有极限,就可以用商的极限运用法则计算。
总结: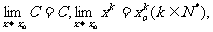
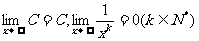
例6 求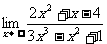
分析:同例5一样,不能直接用法则求极限. 如果分子、分母都除以 ,就可以运用法则计算了。
,就可以运用法则计算了。
四 课堂练习(利用函数的极限法则求下列函数极限)
(1) ;
(2)
;
(2)
(3)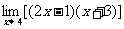 ;
(4)
;
(4)
(5)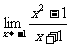 (6)
(6)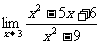
(7)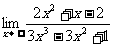 (8)
(8)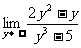
五 小结
1.函数极限存在的条件;如何求函数的极限。
特别地, ;
;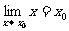
破釜沉舟!!攻克语音关!(22)
|
400 |
痉挛 |
|
410 |
羞赧 |
|
|
401 |
皱缬 |
|
411 |
耄耋 |
|
|
402 |
监生 |
|
412 |
胳臂 |
|
|
403 |
砥柱 |
|
413 |
胼胝 |
|
|
404 |
秘鲁 |
|
414 |
脊梁 |
|
|
405 |
租赁 |
|
415 |
脑髓 |
|
|
406 |
窈窕 |
|
416 |
荷枪 |
|
|
407 |
笑靥 |
|
417 |
荷蓧 |
|
|
408 |
绦虫 |
|
418 |
莅临 |
|
|
409 |
罢黜 |
|
419 |
莞尔 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com