
(16)(本小题12分)
设△ABC的三个内角A、B、C的对边分别为a、b、c,若B=60°,且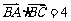 ,
,
(1)求△ABC的面积;
(2)若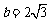 ,求a、c.
,求a、c.
(17)(本小题12分)
17.某校高中篮球兴趣爱好者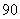 人来进行投篮测试,现假定每人投
人来进行投篮测试,现假定每人投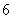 次,每次投中的概率均为
次,每次投中的概率均为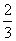 ,且每次投篮的结果都是相互独立的.
,且每次投篮的结果都是相互独立的.
(1)求学生甲在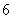 次投篮中投中3次的概率;
次投篮中投中3次的概率;
(2)若某一学生在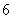 次投篮中至少投中
次投篮中至少投中
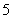 次就被认定为“优秀”,那么试估计这些篮球兴趣爱好者被认定为“优秀”的人数.
次就被认定为“优秀”,那么试估计这些篮球兴趣爱好者被认定为“优秀”的人数.
(18)(本小题12分)
已知菱形ABCD的两条对角线交于点O,且AC=8,BD=4,E 、F分别是BC、CD的中点,将△ABD沿BD折起,使平面ABD⊥平面BDC.
 (1)求证EF⊥平面 AOC;
(1)求证EF⊥平面 AOC;
(2)求AE与平面AOC所成角的正弦值;
(3)求点B到平面AEF的距离.
(19) (本小题满分13分)
某种商品的生产成本为50元/件,出厂价为60元/件.厂家为了鼓励销售商多订购,决定当一次性订购超过100件时,每多订购一件,所订购全部商品的出厂价就降低0.01元.根据市场调查,销售商一次订购不会超过600件.
(1)设销售商一次订购x件商品时的出厂价为f(x),请写出f(x)的表达式;
(2)当销售商一次订购多少件商品时,厂家获得的利润最大?最大利润是多少?
(20)(本小题满分13分)
已知椭圆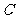 的中心在原点,焦点
的中心在原点,焦点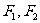 在
在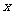 轴上,离心率
轴上,离心率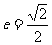 ,且经过点
,且经过点 。
。
(1)求椭圆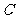 的方程;
的方程;
 (2) 若直线
(2) 若直线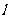 经
经 过椭圆
过椭圆 的右焦点
的右焦点 ,且与椭圆
,且与椭圆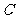 交于
交于 两点,使得
两点,使得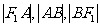 依次成等差数列,求直线
依次成等差数列,求直线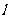 的方程。
的方程。
(21)(本小题13分)
已知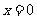 是函数
是函数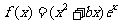 的一个极值点.
的一个极值点.
(1)求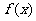 ;
(2)若不等式
;
(2)若不等式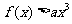 在[
在[ ,2]内有解,求实数
,2]内有解,求实数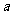 的取值范围;
的取值范围;
(3)函数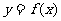 在
在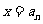 (
(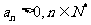 )处的切线与
)处的切线与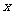 轴的交点为(
轴的交点为(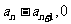 ).若
).若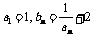 ,问是否存在等差数列{
,问是否存在等差数列{ },使得b1c1+b2c2+…+bncn=2n+1(2n-1)
},使得b1c1+b2c2+…+bncn=2n+1(2n-1)
+n2+2n+2对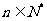 都成立?若存在求出{
都成立?若存在求出{ }的通项公式,若不存在,请说明理由.
}的通项公式,若不存在,请说明理由.
湖南省常德市2010届高三下学期4月月考
15.定义区间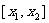 的长度为
的长度为 ,已知函数
,已知函数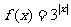 的定义域为
的定义域为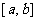 ,值域为
,值域为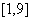 ,则区间
,则区间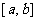 的长度的最大值为 ,最小值为 .
的长度的最大值为 ,最小值为 .
14.设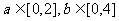 ,则函数
,则函数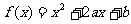 在
在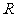 上有两个不同零点的概率为
.
上有两个不同零点的概率为
.
13.已知正数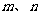 满足
满足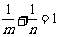 ,则
,则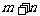 的最小值为 .
的最小值为 .
12.若直线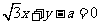 与圆
与圆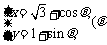 为参数)没有公共点,则
为参数)没有公共点,则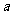 的取值范围是
.
的取值范围是
.
11.已知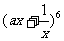 的展开式中常数项为20,则
的展开式中常数项为20,则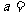 .
.
10.某校有教师100人,男学生600人,女学生500人,现用分层抽样的方法从所有师生中抽出一个容量为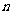 的样本.已知从女生中抽取的人数为40人,则
的样本.已知从女生中抽取的人数为40人,则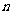 =
.
=
.
9.若复数( )2=a+bi(a、
)2=a+bi(a、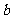 为实数)则
为实数)则 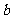 = .
= .
8.已知函数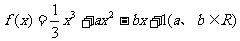 在区间
在区间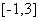 上是减函数,则
上是减函数,则 的最小值是
的最小值是
A. 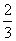 B.
B. 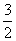 C.2 D. 3
C.2 D. 3
第Ⅰ卷答题处,将正确答案前的字母填入下表相应的空格内.
|
题 目 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
答案代号 |
2 |
|
|
|
|
|
|
|
登分栏(由评卷教师填写)
第Ⅱ卷(非选择题共110分)
7.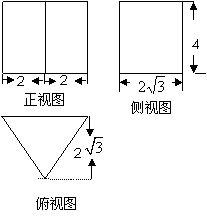 某几何体的三视图如下,根据图中标出的
某几何体的三视图如下,根据图中标出的
尺寸,可得这个几何体的体积为
A.12
B.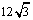
C.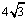
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com