
22、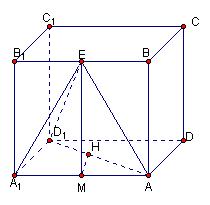 正四棱柱
正四棱柱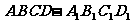 中,底面边长为
中,底面边长为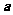 ,侧棱长为
,侧棱长为 ,
,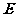 为棱
为棱 的中点,记以
的中点,记以 为棱,
为棱, ,
, 为面的二面角大小为
为面的二面角大小为 ,
,
(1)是否存在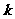 值,使直线
值,使直线 平面
平面 ,
,
若存在,求出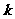 值;若不存在,说明理由;
值;若不存在,说明理由;
(2)试比较 与
与 的大小。
的大小。
21、已知:如图,矩形 ,
, 平面
平面 ,
,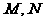 分别是
分别是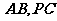 的中点,
的中点,
(1)求证:直线 直线
直线 ,
,
(2)若平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为 ,能否确定
,能否确定 使直线
使直线 是异面直线
是异面直线 与
与 的公垂线.若能确定,求出
的公垂线.若能确定,求出 的值;若不能确定,说明理由。
的值;若不能确定,说明理由。

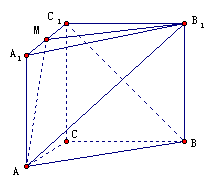
20、已知正三棱柱 的每条棱长均为
的每条棱长均为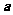 ,
,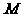 为棱
为棱 上的动点,
上的动点,
(1)当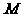 在何处时,
在何处时, ∥平面
∥平面 ,并证明之;
,并证明之;
(2)在(1)下,求平面 与平面
与平面 所成锐二面角的正切值。
所成锐二面角的正切值。
19、美国篮球职业联赛( ),某赛季的总决赛在洛杉矶湖人队与费城76人队之间角逐,采用七局四胜制,即若有一队胜四场,由此队获胜且比赛结束,因两队实力水平非常接近,在每场比赛中两队获胜是等可能的,据以往资料统计,每场比赛组织者可获门票收入300万美元,两队决出胜负后问:
),某赛季的总决赛在洛杉矶湖人队与费城76人队之间角逐,采用七局四胜制,即若有一队胜四场,由此队获胜且比赛结束,因两队实力水平非常接近,在每场比赛中两队获胜是等可能的,据以往资料统计,每场比赛组织者可获门票收入300万美元,两队决出胜负后问:
(1)组织者在此次决赛中获门票收入为1200万美元的概率是多少?
(2)组织者在此次决赛中获门票收入不低于1800万美元的概率是多少?
18、(甲)在三棱柱 中,
中, ,
, 分别是
分别是
 的中点,
G是
的中点,
G是 上的点,
上的点,
(1)如果 ,试确定点
,试确定点 的位置;
的位置;
(2)在满足条件(1)的情况下,试求 的值。
的值。

(乙)正方体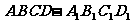 中,
中,
(1)在棱 上有一点
上有一点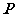 ,当
,当 为多少时,使二面角
为多少时,使二面角 的大小等于
的大小等于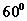 ;
;
 (2)在(1)的条件下,求直线
(2)在(1)的条件下,求直线 所成的角。
所成的角。
17、在三棱柱 ,已知
,已知 是正方形且边长为
是正方形且边长为 ,
, 为矩形,且平面
为矩形,且平面 ⊥平面
⊥平面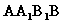
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求点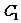 到平面
到平面 的距离。
的距离。

16、椭圆 的两焦点为
的两焦点为 ,现将坐标平面沿
,现将坐标平面沿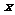 轴折成二面角,二面角的度数为
轴折成二面角,二面角的度数为 ,已知折起后两焦点的距离
,已知折起后两焦点的距离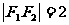 ,则满足题设的一组数值:
,则满足题设的一组数值:
 (只需写出一组就可以,不必写出所有情况)
(只需写出一组就可以,不必写出所有情况)
15、甲、乙两名射击运动员,甲命中10环的概率为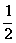 ,乙命中10环的概率为
,乙命中10环的概率为 ,若他们各射击两次,甲比乙命中10环次数多的概率恰好等于
,若他们各射击两次,甲比乙命中10环次数多的概率恰好等于 ,则
,则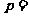 。
。
14、一排共9个座位,甲、乙、丙三人按如下方式入座,每人左、右两旁都有空座位,且甲必须在乙、丙两人之间,则不同的坐法共有 种。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com