
1.先后抛掷2枚均匀硬币,出现2枚反面的概率是( )
A.1 B.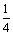 C.
C.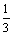 D.
D.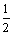
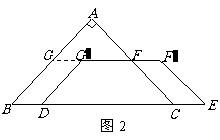
1、(2010年泉州南安市)如图1,在 中,
中,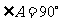 ,
,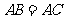 ,
,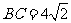 ,另有一等腰梯形
,另有一等腰梯形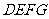 (
(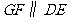 )的底边
)的底边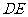 与
与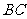 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
(1)直接写出△AGF与△ABC的面积的比值;
(2)操作:固定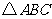 ,将等腰梯形
,将等腰梯形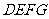 以每秒1个单位的速度沿
以每秒1个单位的速度沿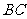 方向向右运动,直到点
方向向右运动,直到点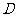 与点
与点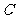 重合时停止.设运动时间为
重合时停止.设运动时间为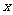 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为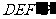 (如图2).
(如图2).
①探究1:在运动过程中,四边形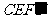 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时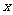 的值;若不能,请说明理由.
的值;若不能,请说明理由.
 ②探究2:设在运动过程中
②探究2:设在运动过程中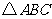 与等腰梯形
与等腰梯形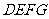 重叠部分的面积为
重叠部分的面积为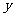 ,求
,求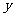 与
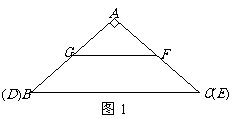
与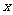 的函数关系式.
的函数关系式.
19.规律和有理数里均有(10湖南怀化)有一组数列:2,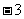 ,2,
,2,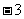 ,2,
,2,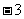 ,2,
,2,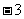 ,…… ,根据这个规律,那么第2010个数是______.-3
,…… ,根据这个规律,那么第2010个数是______.-3
16.(2010年眉山)如图,将第一个图(图①)所示的正三角形连结各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,……,则得到的第五个图中,共有________个正三角形.
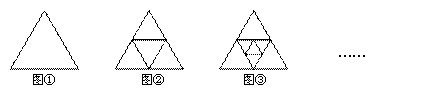
答案:17
 北京12. 右图为手的示意图,在各个手指间标记字母A、B、C、D。请你按图中箭头
北京12. 右图为手的示意图,在各个手指间标记字母A、B、C、D。请你按图中箭头
所指方向(即A®B®C®D®C®B®A®B®C®…的方式)从A开始数连续的
正整数1,2,3,4…,当数到12时,对应的字母是 ;当字母C第201
次出现时,恰好数到的数是 ;当字母C第2n+1次出现时(n为正整数),
恰好数到的数是 (用含n的代数式表示)。

北京25. 问题:已知△ABC中,ÐBAC=2ÐACB,点D是△ABC内的一点,且AD=CD,BD=BA。
探究ÐDBC与ÐABC度数的比值。
请你完成下列探究过程:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明。
(1) 当ÐBAC=90°时,依问题中的条件补全右图。
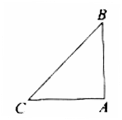 观察图形,AB与AC的数量关系为 ;
观察图形,AB与AC的数量关系为 ;
当推出ÐDAC=15°时,可进一步推出ÐDBC的度数为 ;
可得到ÐDBC与ÐABC度数的比值为 ;
(2) 当ÐBAC¹90°时,请你画出图形,研究ÐDBC与ÐABC度数的比值
是否与(1)中的结论相同,写出你的猜想并加以证明。

24.(2010年成都)已知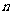 是正整数,
是正整数,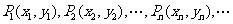 是反比例函数
是反比例函数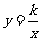 图象上的一列点,其中
图象上的一列点,其中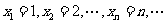 .记
.记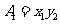 ,
,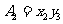 ,
,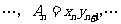 若
若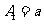 (
( 是非零常数),则
是非零常数),则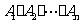 的值是________________________(用含
的值是________________________(用含 和
和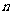 的代数式表示).
的代数式表示).
答案: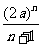
25.(2010宁波市)十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式请你观察下列几种简单多面体模型,解答下列问题:
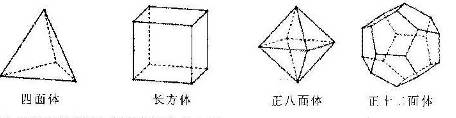
(1)根据上面多面体的模型,完成表格中的空格:
|
多面体 |
顶点数(V) |
面数(F) |
棱数(E) |
|
四面体 |
4 |
4 |
|
|
长方体 |
8 |
6 |
12 |
|
正八面体 |
|
8 |
12 |
|
正十二面体 |
20 |
12 |
30 |
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是________;
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是;
(3)某个玻璃饰品的外形是简单的多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x个,八边形的个数为y,求x+y的值.
17.(2010年连云港)如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为,再分别取A1C、B1C的中点A2、B2,A2C、B2C的中点A3、B3,依次取下去….利用这一图形,能直观地计算出+++…+=________.

(2010济宁市)18.(6分)观察下面的变形规律:
 =1-
=1-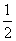 ;
;
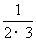 =
=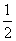 -
-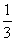 ;
;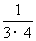 =
=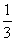 -
-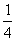 ;……
;……
解答下面的问题:
(1)若n为正整数,请你猜想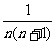 = ;
= ;
(2)证明你猜想的结论;
(3)求和: +
+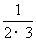 +
+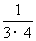 +…+
+…+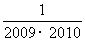 .
.
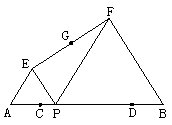
18.(桂林2010)如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.3
22.(玉溪市2010) 平面内的两条直线有相交和平行两种位置关系.
(1)AB平行于CD.如图a,点P在AB、CD外部时,由AB∥CD,有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D.如图b,将点P移到AB、CD内部,以上结论是否成立?,若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
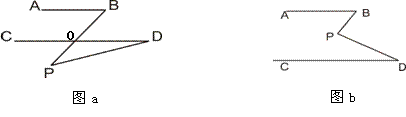
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,
如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
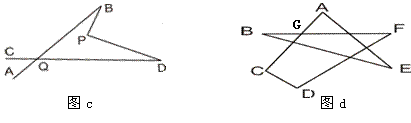 |
|||
|
|||
解:(1)不成立,结论是∠BPD=∠B+∠D.
延长BP交CD于点E,
∵AB∥CD. ∴∠B=∠BED.
又∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D. …………4分
(2)结论: ∠BPD=∠BQD+∠B+∠D. …………7分
(3)由(2)的结论得:∠AGB=∠A+∠B+∠E.
又∵∠AGB=∠CGF.
∠CGF+∠C+∠D+∠F=360°
∴∠A+∠B+∠C+∠D∠E+∠F=360°. …………11分
1.(2010哈尔滨)观察下列图形:

它们是按一定规律排列的,依照此规律,第9个图形中共有 个★28
(2010红河自治州)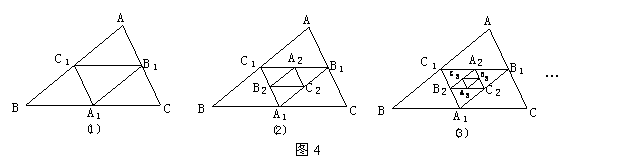 15. 如图4,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1
A1、 A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有 3n 个.
15. 如图4,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1
A1、 A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有 3n 个.
(2010遵义市)小明玩一种的游戏,每次挪动珠子的颗数与对应所得的分数如下表:
当对应所得分数为132分时,则挪动的珠子数为 ▲ 颗.
答案:12
(2010台州市)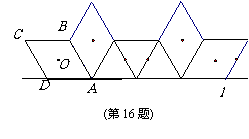 如图,菱形ABCD中,AB=2 ,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O所经过的路径总长为(结果保留π) ▲ .
如图,菱形ABCD中,AB=2 ,∠C=60°,菱形ABCD在直线l上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O所经过的路径总长为(结果保留π) ▲ .
答案:8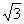 +4)π
+4)π
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com