
20.(本小题满分14分)
我们把半椭圆 与圆弧
与圆弧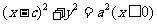 合成的曲线称作“曲圆”,其中
合成的曲线称作“曲圆”,其中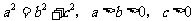 。如图,
。如图, 为半椭圆的右焦点,
为半椭圆的右焦点, 和
和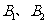 分别是“曲圆”与
分别是“曲圆”与 轴、
轴、 轴的焦点,已知
轴的焦点,已知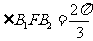 ,扇形
,扇形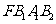 的面积等于
的面积等于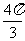 。
。
(Ⅰ)求“曲圆”的方程;
(Ⅱ)过点F倾斜角为 的直线交“曲圆”于
的直线交“曲圆”于 两点,试将
两点,试将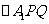 的周长
的周长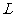 表示为
表示为 的函数;
的函数;
(Ⅲ)当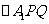 的周长
的周长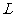 最大时,试探究
最大时,试探究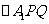 的面积
的面积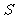 是否为定值?若是,求出
是否为定值?若是,求出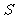 的值;若不是,求出
的值;若不是,求出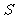 的取值范围。
的取值范围。

19.(本小题满分13分)
已知函数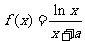 (
( 为常数)在点
为常数)在点 处切线的斜率为
处切线的斜率为 。
。
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若函数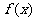 在区间
在区间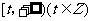 上存在极值,求
上存在极值,求 的最大值;
的最大值;
(Ⅲ)设 ,试问数列
,试问数列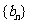 中是否存在
中是否存在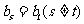 ?若存在,求出所有相等的两项;若不存在,请说明理由
?若存在,求出所有相等的两项;若不存在,请说明理由
18.(本小题满分13分)
图1是长方体截去一个角后得到的几何体,其中底面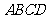 是正方形,
是正方形,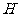 为
为 中点,图2是该几何体的侧视图。
中点,图2是该几何体的侧视图。
(Ⅰ)判断两直线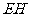 与
与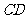 的位置关系,并给予证明;
的位置关系,并给予证明;
(Ⅱ)求直线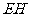 与平面
与平面 所成角的大小;
所成角的大小;
(Ⅲ)是否存在点 ,使得
,使得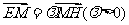 ,且二面角
,且二面角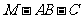 的大小为
的大小为 ?若存在,求不存在,请说明理由。
?若存在,求不存在,请说明理由。

17.(本小题满分13分)
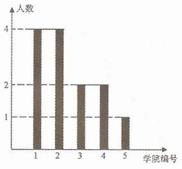
上海世博会举办时间为2010年5月1日-10月31日。福建馆以“海西”为参博核心元素,主题为“潮涌海西,魅力福建”。福建馆招募了60名志愿者,某高校有l3人入选,其中5人为中英文讲解员,8人为迎宾礼仪,它们来自该校的5所所学院(这5所学院编号为1-5号),人员分布如图所示。
若从这13名入选者中随机抽取3人。
(Ⅰ)求这3人所在学院的编号恰好成等比数列的概率;
(Ⅱ)求这3人中中英文讲解员人数的分布列及数学期望。
16.(本小题满分13分)
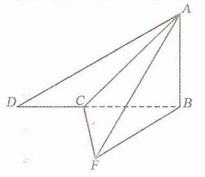 如图,为测量鼓浪屿郑成功雕像
如图,为测量鼓浪屿郑成功雕像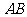 的高度及取景点
的高度及取景点 与
与 之间的距离(
之间的距离(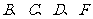 在同一水平面上,雕像垂直该水平面于点
在同一水平面上,雕像垂直该水平面于点 ,且
,且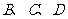 三点共线),某校研究性学习小组同学在
三点共线),某校研究性学习小组同学在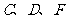 三点处测得顶点
三点处测得顶点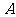 的仰角分别为45°、30°、
的仰角分别为45°、30°、
30°。若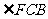 =60°,
=60°,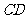 =
=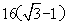 米。
米。
(Ⅰ)求雕像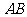 的高度;
的高度;
(Ⅱ)求取景点 与
与 之间的距离。
之间的距离。
15.已知数列 的通项公式为
的通项公式为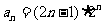 ,我们用错位相减法求其前
,我们用错位相减法求其前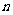 项和
项和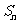 :
:
由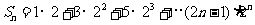 得
得
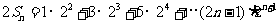
两式项减得: ,
,
求得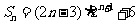 。类比推广以上方法,若数列
。类比推广以上方法,若数列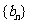 的通项公式为
的通项公式为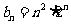 ,
,
则其前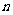 项和
项和 。
。
14.函数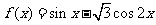 的图象向左平移
的图象向左平移 个单位(
个单位( ),若所得图象对应的函数为偶函数,则
),若所得图象对应的函数为偶函数,则 的最小值为
。
的最小值为
。
13.将一枚均匀硬币连续掷十次,记事件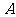 为“第一、三、五、七、九次是正面向上,第二、四、六、八、十次是反面向上”,记事件
为“第一、三、五、七、九次是正面向上,第二、四、六、八、十次是反面向上”,记事件 为“十次都是正面向上”,则这两个事件发生的概率
为“十次都是正面向上”,则这两个事件发生的概率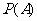 与
与 的大小关系是
。
的大小关系是
。
12.定积分 。
。
11.在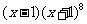 的展开式中,含
的展开式中,含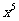 项的系数是
。
项的系数是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com