
1、
已知等差数列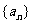 中,
中,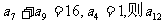 的值是 ( )
的值是 ( )
A 15 B 30 C 31 D 64
8.已知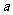 为实数,
为实数,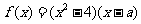 ,
,
(1)求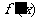 ;
;
(2)若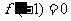 ,求
,求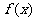 在
在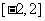 上的最大值和最小值;
上的最大值和最小值;
(3)若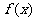 在
在 和
和 上都是递增的,求
上都是递增的,求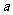 的取值范围.
的取值范围.
7.已知函数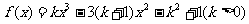 .
.
(1)若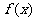 的单调减区间为
的单调减区间为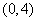 ,求
,求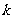 的值;
的值;
(2)当 时,求证:
时,求证: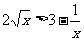 .
.
6.已知函数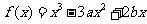 在点
在点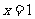 处有极小值
处有极小值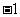 ,试确定
,试确定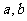 的值,并求出
的值,并求出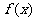 的单调区间.
的单调区间.
5.已知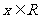 ,奇函数
,奇函数 在
在 上单调,则字母
上单调,则字母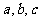 应满足的条件是
.
应满足的条件是
.
4.抛物线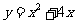 上一点
上一点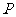 处的切线的倾斜角为
处的切线的倾斜角为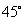 ,切线与
,切线与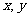 轴的交点分别是
轴的交点分别是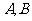 ,则
,则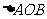 的面积为
.
的面积为
.
3.已知曲线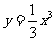 上一点
上一点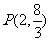 ,则点
,则点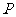 处的切线方程是
;过点
处的切线方程是
;过点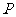 的切线方程是
.
的切线方程是
.
答:点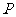 处的切线方程是
处的切线方程是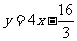 ,过点
,过点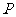 的切线方程是
的切线方程是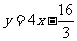 或
或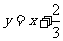 .
.
2.若函数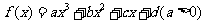 在
在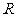 上无极值,则必有 ( )
上无极值,则必有 ( )
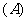
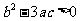
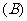
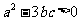
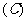
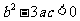
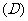
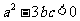
1.设函数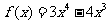 则下列结论中,正确的是 ( )
则下列结论中,正确的是 ( )
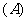
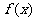 有一个极大值点和一个极小值点
有一个极大值点和一个极小值点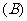
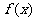 只有一个极大值点
只有一个极大值点
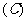
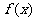 只有一个极小值点
只有一个极小值点 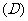
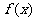 有二个极小值点
有二个极小值点
例1.已知函数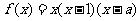 有绝对值相等,符号相反的极大值和极小值,试确定常数
有绝对值相等,符号相反的极大值和极小值,试确定常数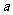 的值.
的值.
解: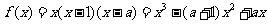 ,
,
∴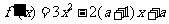 ,
,
令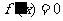 ,得
,得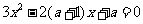 ,
,
由题意,该方程必定有不相等两实根,可分别设为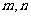 ,
,
则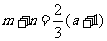 ,
,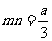 ,
,
∴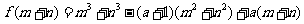
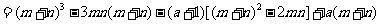
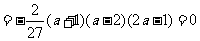
∴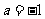 或
或 或
或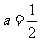 .
.
例2.一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
解:设船速度为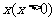 时,燃料费用为
时,燃料费用为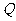 元,则
元,则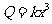 ,
,
由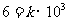 可得
可得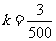 ,∴
,∴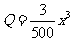 ,
,
∴总费用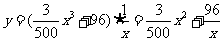 ,
,
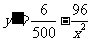 ,令
,令 得
得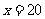 ,
,
当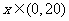 时,
时, ,此时函数单调递减,
,此时函数单调递减,
当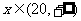 时,
时, ,此时函数单调递增,
,此时函数单调递增,
∴当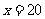 时,
时,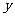 取得最小值,
取得最小值,
∴此轮船以20公里/小时的速度使行驶每公里的费用总和最小.
例3.如图,已知曲线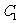 :
:
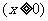 与曲线
与曲线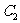 :
: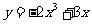
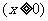 交于点
交于点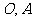 ,直线
,直线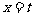
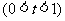 与曲线
与曲线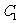 、
、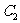 交于点
交于点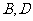 ,
,
(1)写出四边形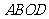 的面积
的面积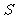 与
与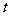 的函数关系
的函数关系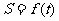 ;
;
(2)讨论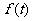 的单调性,并求
的单调性,并求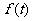 的最大值.
的最大值.
解:(1)由 得交点
得交点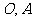 坐标分别是
坐标分别是 ,
,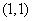 ,
,
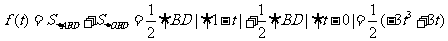 ,
,
 ∴
∴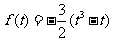
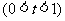 .
.
(2)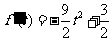 ,令
,令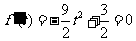 ,得
,得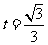 ,
,
当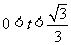 时,
时,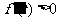 ,此时函数在
,此时函数在 单调递增;
单调递增;
当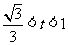 时,
时,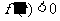 ,此时函数在
,此时函数在 单调递减.
单调递减.
所以,当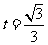 时,
时,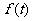 的最大值为
的最大值为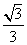 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com