
21.(本题满分14分)
已知椭圆 的离心率为
的离心率为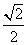 ,椭圆上任意一点到右焦点
,椭圆上任意一点到右焦点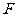 的距离的最大值为
的距离的最大值为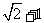 。
。
(1)求椭圆的方程;
(2)已直点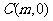 是线段
是线段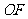 上一个动点(
上一个动点(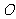 为坐标原点),是否存在过点
为坐标原点),是否存在过点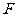 且与
且与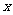 轴不垂直的直线
轴不垂直的直线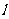 与椭圆交于
与椭圆交于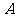 、
、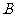 两点,使得
两点,使得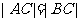 ,并说明理由。
,并说明理由。
20.(本题满分14分)
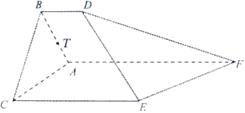
如图所示的几何体是以正三角形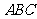 为底面的直棱柱(侧棱垂直于底面的棱柱)被平
为底面的直棱柱(侧棱垂直于底面的棱柱)被平
面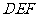 所截而得,
所截而得,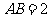 ,
,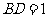 ,
,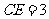 ,
,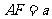 ,
,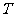 为
为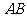 的中点。
的中点。
(1)当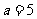 时,求证:
时,求证: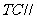 平面
平面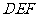 ;
;
(2)当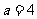 时,求平面
时,求平面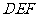 与平面
与平面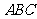 相交所成且为锐角的二面角的余弦值;
相交所成且为锐角的二面角的余弦值;
(3)当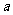 为何值时,在
为何值时,在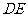 上存在点
上存在点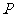 ,使
,使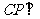 平面
平面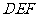 ?
?
19.(本题满分14分)
某校篮球选修课的考核方式采用远距离投篮进行,规定若学生连中二球,则通过考核,终止投篮;否则继续投篮,直至投满四次终止,现有某位同学每次投篮的命中率为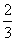 ,且每次投篮相互独立。
,且每次投篮相互独立。
(I)该同学投中二球但未能通过考核的概率;
(Ⅱ)现知该校选修篮球的同学共27位,每位同学每次投篮的命中率为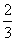 ,且每次投篮相互独立。在这次考核中,记通过考核的人数为X,求X的期望。
,且每次投篮相互独立。在这次考核中,记通过考核的人数为X,求X的期望。
18.(本题满分14分)
已知向量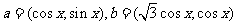 ,若
,若
(I)求函数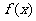 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(Ⅱ)求函数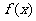 在区间
在区间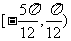 上的值域。
上的值域。
17.定义在(-1,1)上的函数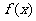 满足:
满足:
(i)对任意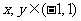 有
有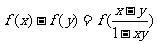 ,
,
(ii)当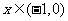 时,有
时,有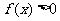 ;
;
若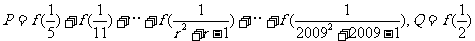 ,
, ;则
;则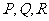 的大小关系为_______(用“<”连接)
的大小关系为_______(用“<”连接)
16.曲线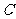 由
由 和
和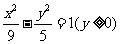 两部分组成,若过点(0,2)作直线
两部分组成,若过点(0,2)作直线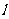 与曲线
与曲线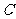 有且仅有两个公共点,则直线
有且仅有两个公共点,则直线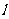 的斜率的取值范围为__________。
的斜率的取值范围为__________。
15.若 ,则
,则 的最大值为
的最大值为
__________。
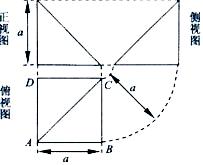
14.四棱锥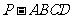 的顶点
的顶点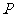 在底面
在底面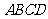 中的
中的
投影恰好是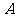 ,其三视图如右图,则四棱锥
,其三视图如右图,则四棱锥
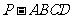 的表面积为____________。
的表面积为____________。
13. 在
在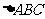 中,
中,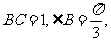 当
当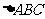 的面
的面
积等于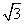 时,
时,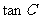 等于_________。
等于_________。
12.右图是2009年CCTV青年歌手电视大奖赛上某一位选手得分的茎叶统
计图,去掉一个最高分和一个最低分后,所剩数据的方差为_______。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com