
4、先后抛掷两枚均匀的正方体骰子(他们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x,y, 则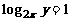 的概率为
的概率为
A.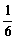 B.
B.
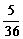 C.
C.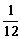 D.
D.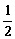
3、记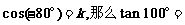
A. 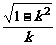 B.
B.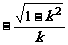 C.
C. D.
D.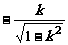
2、设向量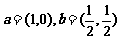 ,则下列结论中正确的是
,则下列结论中正确的是
A. 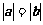 B.
B.
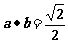 C.
C.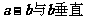 D.
D.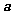 ∥
∥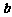
1、计算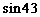 º
º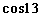 º
º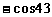 º
º º的结果等于
º的结果等于
A. 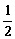 B.
B.
 C.
C.
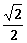 D.
D.
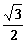
3.预习:课本P35-36内容.
2.设A是C的充分条件,B是C的充分条件,D是C的必要条件,D是B的充分条件,那么,D是A的什么条件?A是B的什么条件?
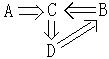 解:由题意作出逻辑图(右图),便知,
解:由题意作出逻辑图(右图),便知,
D是A的必要条件;A是B的充分条件.
1.课本P34-35内容,熟悉巩固有关内容.
本节主要学习了推断符号“ ”的意义,充分条件与必要条件的概念,以及判断充分条件与必要条件的方法.
”的意义,充分条件与必要条件的概念,以及判断充分条件与必要条件的方法.
判断充分条件与必要条件的依据是:
若p q(或若┐q
q(或若┐q ┐p),则p是q的充分条件;
┐p),则p是q的充分条件;
若q p(或若┐p
p(或若┐p ┐q),则p是q的必要条件.
┐q),则p是q的必要条件.
(补充题)用“充分”或“必要”填空,并说明理由:
⒈“a和b都是偶数”是“a+b也是偶数”的 充分 条件;
⒉“四边相等”是“四边形是正方形”的 必要 条件;
⒊“x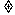 3”是“|x|
3”是“|x|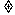 3”的
充分 条件;
3”的
充分 条件;
⒋“x-1=0”是“x2-1=0”的 充分 条件;
⒌“两个角是对顶角”是“这两个角相等”的 充分 条件;
⒍“至少有一组对应边相等”是“两个三角形全等”的必要条件;
⒎对于一元二次方程ax2+bx+c=0(其中a,b,c都不为0)来说,“b2-4ac 0”是“这个方程有两个正根”的
必要 条件;
0”是“这个方程有两个正根”的
必要 条件;
⒏“a=2,b=3”是“a+b=5”的 充分 条件;
⒐“a+b是偶数”是“a和b都是偶数”的 必要 条件;
⒑“个位数字是5的自然数”是“这个自然数能被5整除”的
充分 条件.
例1 指出下列各组命题中,p是q的什么条件,q是p的什么条件:
⑴ p:x=y;q:x2=y2.
⑵ p:三角形的三条边相等;q:三角形的三个角相等.
分析:可根据“若p则q”与“若q则p”的真假进行判断.
解:⑴由p q,即x=y
q,即x=y x2=y2,知p是q的充分条件,q是p的必要条件.
x2=y2,知p是q的充分条件,q是p的必要条件.
⑵由p q,即三角形的三条边相等
q,即三角形的三条边相等 三角形的三个角相等,知p是q的充分条件,q是p的必要条件;
三角形的三个角相等,知p是q的充分条件,q是p的必要条件;
又由q p,即三角形的三个角相等
p,即三角形的三个角相等 三角形的三条边相等,知q也是p的充分条件,p也是q的必要条件.
三角形的三条边相等,知q也是p的充分条件,p也是q的必要条件.
练习:课本P35练习:2⑴⑵⑶⑷.
答案:⑴∵p q,∴p是q的充分条件,q是p的必要条件;
q,∴p是q的充分条件,q是p的必要条件;
⑵∵q p,∴p是q的必要条件,q是p的充分条件;
p,∴p是q的必要条件,q是p的充分条件;
⑶∵p q,∴p是q的充分条件,q是p的必要条件;又∵q
q,∴p是q的充分条件,q是p的必要条件;又∵q p,∴q也是p的充分条件,p也是q的必要条件.
p,∴q也是p的充分条件,p也是q的必要条件.
⑷∵p q,∴p是q的充分条件,q是p的必要条件;又∵q
q,∴p是q的充分条件,q是p的必要条件;又∵q p,∴q也是p的充分条件,p也是q的必要条件.
p,∴q也是p的充分条件,p也是q的必要条件.
以上是直接利用定义由原命题判断充分条件与必要条件的方法.那么,如果由命题不是很好判断的话,我们可以换一种方式,根据互为逆否命题的等价性,利用它的逆否命题来进行判断.
2. 利用逆否命题判断:即“若┐q
利用逆否命题判断:即“若┐q ┐p成立,则p是q的充分条件,q是p的必要条件”.
┐p成立,则p是q的充分条件,q是p的必要条件”.
例2(补)如图1,有一个圆A,在其内又含有一个圆B. 请回答:
⑴命题:若“A为绿色”,则“B为绿色”中,“A为绿色”是“B为绿色”的什么条件;“B为绿色”又是“A为绿色”的什么条件.
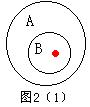 ⑵命题:若“红点在B内”,则“红点一定在A内”中,“红点在B内”是“红点在A内”的什么条件;“红点在A内”又是“红点在B内”的什么条件.
⑵命题:若“红点在B内”,则“红点一定在A内”中,“红点在B内”是“红点在A内”的什么条件;“红点在A内”又是“红点在B内”的什么条件.
解法1(直接判断):⑴∵“A为绿色 B为绿色”是真的,∴由定义知,“A为绿色”是“B为绿色”的充分条件;“B为绿色”是“A为绿色”的必要条件.
B为绿色”是真的,∴由定义知,“A为绿色”是“B为绿色”的充分条件;“B为绿色”是“A为绿色”的必要条件.
⑵如图2⑴,∵“红点在B内 红点在A内”是真的,∴由定义知,“红点在B内”是“红点在A内”的充分条件;“红点在A内”是“红点在B内”的必要条件.
红点在A内”是真的,∴由定义知,“红点在B内”是“红点在A内”的充分条件;“红点在A内”是“红点在B内”的必要条件.
解法2(利用逆否命题判断):⑴它的逆否命题是:若“B不为绿色”则“A不为绿色”. ∵“B不为绿色
 A不为绿色”为真,∴“A为绿色”是“B为绿色”的充分条件;“B为绿色”是“A为绿色”的必要条件.
A不为绿色”为真,∴“A为绿色”是“B为绿色”的充分条件;“B为绿色”是“A为绿色”的必要条件.
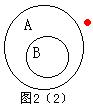 ⑵它的逆否命题是:若“红点不在A内”,则“红点一定不在B内”. 如图2⑵,∵“红点不在A内
⑵它的逆否命题是:若“红点不在A内”,则“红点一定不在B内”. 如图2⑵,∵“红点不在A内 红点一定不在B内”为真,∴“红点在B内”是“红点在A内”的充分条件;“红点在A内”是“红点在B内”的必要条件.
红点一定不在B内”为真,∴“红点在B内”是“红点在A内”的充分条件;“红点在A内”是“红点在B内”的必要条件.
如何理解充分条件与必要条件中的“充分”和“必要”呢?下面我们以例2为例来说明.
先说充分性:说条件是充分的,也就是说条件是充足的,条件是足够的,条件是足以保证的.例如,说“A为绿色”是“B为绿色”的一个充分条件,就是说“A为绿色”,它足以保证“B为绿色”.它符合上述的“若p则q”为真(即p q)的形式.
q)的形式.
再说必要性:必要就是必须,必不可少.从例2的图可以看出,如果“B为绿色”,A可能为绿色,A也可能不为绿色.但如果“B不为绿色”,那么“A不可能为绿色”.因此,必要条件简单说就是:有它不一定,没它可不行.它满足上述的“若非q则非p”为真(即┐q ┐p)的形式.
┐p)的形式.
总之,数学上的充分条件、必要条件的“充分”、“必要”两词,与日常生活中的“充分”、“必要”意义相近,不过,要准确理解它们,还是应该以数学定义为依据.
例2的问题,若用集合观点又怎样解释呢?请同学们想一想.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com