
21.[选做题]在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
A.选修4-1 几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,且CA平分∠BAF,过点C作CD⊥AF
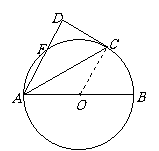 交AF的延长线于点D. 求证:DC是⊙O的切线.
交AF的延长线于点D. 求证:DC是⊙O的切线.
[证明]连结OC,所以∠OAC=∠OCA.
又因为CA平分∠BAF,所以∠OAC=∠FAC,
于是∠FAC=∠OCA,所以OC//AD.
又因为CD⊥AF,所以CD⊥OC,
故DC是⊙O的切线. ………………… 10分
B.选修4-2 矩阵与变换
变换T是绕坐标原点逆时针旋转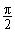 的旋转变换,求曲线
的旋转变换,求曲线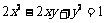 在变换T作用
在变换T作用
下所得的曲线方程.
[解]变换T所对应变换矩阵为 ,设
,设 是变换后图像上任一点,与之对应的变换前的点是
是变换后图像上任一点,与之对应的变换前的点是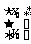 ,则
,则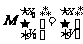 ,即
,即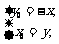 ,代入
,代入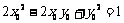 ,
,
即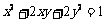 ,
,
所以变换后的曲线方程为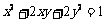 .
………………… 10分
.
………………… 10分
C.选修4-4 参数方程与极坐标(本题满分10分)
已知圆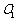 和圆
和圆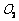 的极坐标方程分别为
的极坐标方程分别为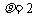 ,
,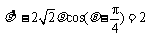 .
.
(1)把圆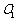 和圆
和圆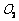 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
[解](1)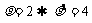 ,所以
,所以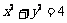 ;因为
;因为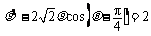 ,
,
所以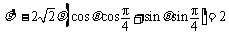 ,所以
,所以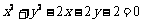 . ………5分
. ………5分
(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为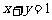 .
.
化为极坐标方程为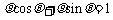 ,即
,即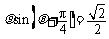 . ………………… 10分
. ………………… 10分
D.选修4-5 不等式证明选讲(本题满分10分)
已知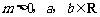 ,求证:
,求证: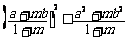 .
.
[解]因为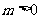 ,所以
,所以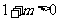 ,所以要证
,所以要证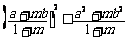 ,
,
即证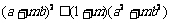 , 即证
, 即证 ,
,
即证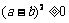 ,而
,而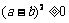 显然成立,故
显然成立,故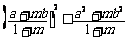 .…………… 10分
.…………… 10分
[必做题]第22题、第23题,每题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
20.(本小题满分16分)
已知二次函数g(x)对任意实数x都满足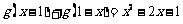 ,且
,且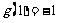 .令
.令
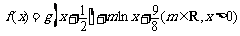 .
.
(1)求 g(x)的表达式;
(2)若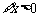 使
使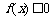 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)设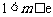 ,
,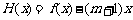 ,
,
证明:对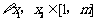 ,恒有
,恒有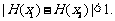
[解]
(1)设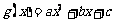 ,于是
,于是
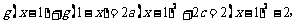 所以
所以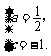
又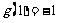 ,则
,则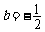 .所以
.所以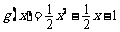 .
……………………4分
.
……………………4分
(2)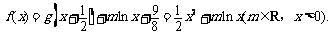
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,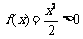 对
对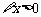 ,
,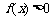 恒成立; ……………………6分
恒成立; ……………………6分
当m<0时,由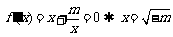 ,列表:
,列表:
|
x |
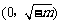 |
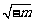 |
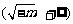 |
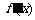 |
- |
0 |
+ |
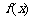 |
减 |
极小 |
增 |
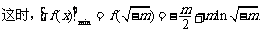
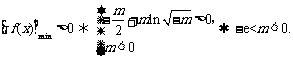 ……………………8分
……………………8分
所以若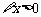 ,
,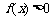 恒成立,则实数m的取值范围是
恒成立,则实数m的取值范围是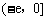 .
.
故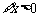 使
使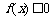 成立,实数m的取值范围
成立,实数m的取值范围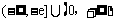 .……………… 10分
.……………… 10分
(3)因为对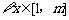 ,
,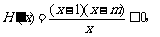 所以
所以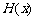 在
在 内单调递减.
内单调递减.
于是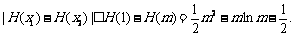
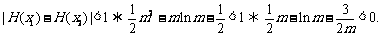 ………………… 12分
………………… 12分
记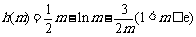 ,
,
则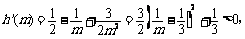
所以函数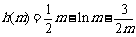 在
在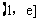 是单调增函数, ………………… 14分
是单调增函数, ………………… 14分
所以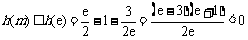 ,故命题成立. ………………… 16分
,故命题成立. ………………… 16分
附加题部分
19.(本小题满分16分)已知椭圆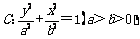 的离心率为
的离心率为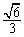 ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且 .
.
(1)求椭圆C和直线l的方程;
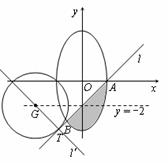
(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若
曲线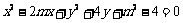 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.
[解](1)由离心率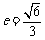 ,得
,得 ,即
,即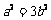 . ① ………………2分
. ① ………………2分
 又点
又点 在椭圆
在椭圆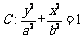 上,即
上,即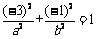 .
② ………………4分
.
② ………………4分
解 ①②得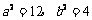 ,
,
故所求椭圆方程为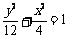 .
…………………6分
.
…………………6分
由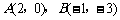 得直线l的方程为
得直线l的方程为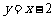 . ………8分
. ………8分
(2)曲线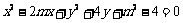 ,
,
即圆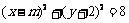 ,其圆心坐标为
,其圆心坐标为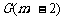 ,半径
,半径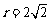 ,表示圆心在直线
,表示圆心在直线
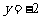 上,半径为
上,半径为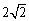 的动圆.
………………… 10分
的动圆.
………………… 10分
由于要求实数m的最小值,由图可知,只须考虑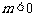 的情形.
的情形.
设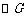 与直线l相切于点T,则由
与直线l相切于点T,则由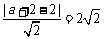 ,得
,得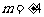 ,………………… 12分
,………………… 12分
当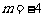 时,过点
时,过点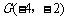 与直线l垂直的直线
与直线l垂直的直线 的方程为
的方程为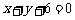 ,
,
解方程组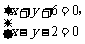 得
得 .
………………… 14分
.
………………… 14分
因为区域D内的点的横坐标的最小值与最大值分别为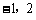 ,
,
所以切点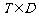 ,由图可知当
,由图可知当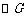 过点B时,m取得最小值,即
过点B时,m取得最小值,即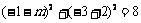 ,
,
解得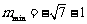 .
…………………
16分
.
…………………
16分
(说明:若不说理由,直接由圆过点B时,求得m的最小值,扣4分)
18.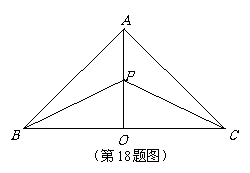 (本小题满分15分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
(本小题满分15分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
(1)设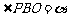 ,把y表示成
,把y表示成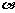 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小区的距离之和最小?
[解](1)在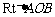 中,
中,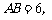 所以
所以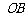 =OA=
=OA=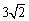 .所以
.所以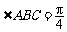
由题意知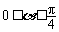 .
……………………2分
.
……………………2分
所以点P到A、B、C的距离之和为
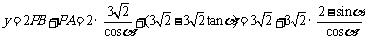 . ……………………6分
. ……………………6分
故所求函数关系式为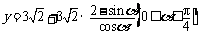 .
……………………7分
.
……………………7分
(2)由(1)得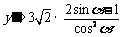 ,令
,令 即
即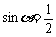 ,又
,又 ,从而
,从而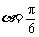 . ……………………9分.
. ……………………9分.
当 时,
时,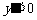 ;当
;当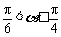 时,
时,  .
.
所以当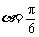 时,
时,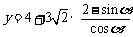 取得最小值,
………………… 13分
取得最小值,
………………… 13分
此时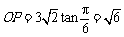 (km),即点P在OA上距O点
(km),即点P在OA上距O点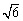 km处.
km处.
[答]变电站建于距O点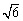 km处时,它到三个小区的距离之和最小. ………… 15分
km处时,它到三个小区的距离之和最小. ………… 15分
17.(本小题满分15分)设等差数列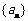 的前
的前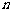 项和为
项和为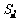 且
且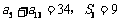 .
.
(1)求数列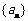 的通项公式及前
的通项公式及前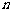 项和公式;
项和公式;
(2)设数列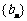 的通项公式为
的通项公式为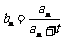 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得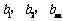
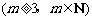 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
[解](1)设等差数列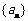 的公差为d. 由已知得
的公差为d. 由已知得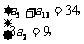 ……………………2分
……………………2分
即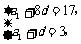 解得
解得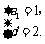 ……………………4分.故
……………………4分.故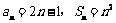 . ………6分
. ………6分
(2)由(1)知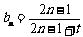 .要使
.要使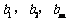 成等差数列,必须
成等差数列,必须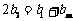 ,即
,即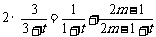 ,……8分.整理得
,……8分.整理得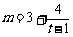 , …………… 11分
, …………… 11分
因为m,t为正整数,所以t只能取2,3,5.当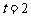 时,
时,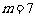 ;当
;当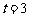 时,
时,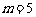 ;当
;当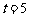 时,
时,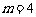 .
.
故存在正整数t,使得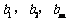 成等差数列. ………………… 15分
成等差数列. ………………… 15分
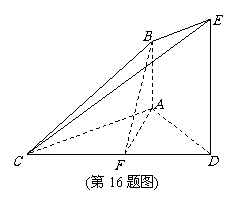
16.(本小题满分14分)如图,已知AB⊥平面ACD,DE⊥平面ACD,AC=AD,DE=2AB,F为CD的中点.
(1) 求证:AF∥平面BCE;
(2) 求证:平面BCE⊥平面CDE.
[证明](1)因为AB⊥平面ACD,DE⊥平面ACD,
所以AB∥DE.
取CE的中点G,连结BG、GF,因为F为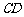 的中点,
的中点,
所以GF∥ED∥BA, GF=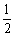 ED=BA,
ED=BA,
从而ABGF是平行四边形,于是AF∥BG. ……………………4分
因为AF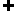 平面BCE,BG
平面BCE,BG 平面BCE,所以AF∥平面BCE. ……………………7分
平面BCE,所以AF∥平面BCE. ……………………7分
(2)因为AB⊥平面ACD,AF 平面ACD,
平面ACD,
所以AB⊥AF,即ABGF是矩形,所以AF⊥GF. ……………………9分
又AC=AD,所以AF⊥CD. ………………… 11分
而CD∩GF=F,所以AF⊥平面GCD,即AF⊥平面CDE.
因为AF∥BG,所以BG⊥平面CDE.
因为BG 平面BCE,所以平面BCE⊥平面CDE.
………………… 14分
平面BCE,所以平面BCE⊥平面CDE.
………………… 14分
15.(本小题满分14分)在△ABC中,a,b,c分别是角A、B、C所对的边,且b2=ac,向量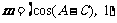 和
和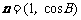 满足
满足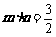 .(1)求
.(1)求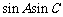 的值;(2)求证:三角形ABC为等边三角形.
的值;(2)求证:三角形ABC为等边三角形.
[解](1)由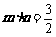 得,
得,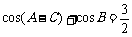 ,
……………………2分
,
……………………2分
又B=π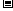 (A+C),得cos(A
(A+C),得cos(A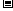 C)
C)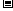 cos(A+C)=
cos(A+C)=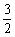 ,
……………………4分
,
……………………4分
即cosAcosC+sinAsinC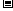 (cosAcosC
(cosAcosC sinAsinC)=
sinAsinC)=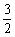 ,所以sinAsinC=
,所以sinAsinC=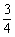 . ……………6分
. ……………6分
[证明](2)由b2=ac及正弦定理得 ,故
,故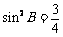 . ……………8分
. ……………8分
于是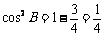 ,所以
,所以 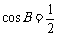 或
或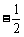 . 因为cosB =
. 因为cosB =
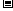 cos(A
cos(A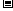 C)>0, 所以
C)>0, 所以 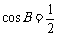 ,故
,故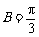 . ………………… 11分
. ………………… 11分
由余弦定理得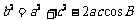 ,即
,即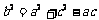 ,又b2=ac,所以
,又b2=ac,所以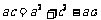 得a=c.
得a=c.
 因为
因为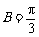 ,所以三角形ABC为等边三角形.
………………… 14分
,所以三角形ABC为等边三角形.
………………… 14分
11.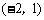 ; 12.4;
13.
; 12.4;
13.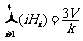 ;
14.0.
;
14.0.
6.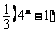 ; 7.
; 7. ;
8.90;
9.10;
10.①③④ ;
;
8.90;
9.10;
10.①③④ ;
1.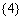 ;
2.
;
2.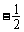 ;
3.2;
4.
;
3.2;
4.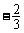 ;
5.
;
5.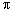 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com