
26.-Shall we attend the concert this evening?
-Great idea, _______ we can do some shopping first.
A. when B. where C. since D. if
25.-Why do English people talk so often about the weather when they start a conversation?
-Well, it’s probably because the weather is a(n)________ topic.
A. safe B. sensitive C. amazing D. ordinary
24. People in Los Angels have no idea of distance on the map, so they measure distance ________
time not miles.
A. by way of B. by means of C. for lack of D. on account of
23.-What kind of food do you prefer?
-______ but Japanese.
-How about Korean, then?
A. Something B. Nothing C. Anything D. Everything
22.-What attracted you to our university?
-You have a great basketball team and I can _______ for it.
A. work out B. look out C. carry out D. try out
23.如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,
AB=BC=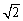 ,BB1=3,D为A1C1的中点,F在线段AA1上.
,BB1=3,D为A1C1的中点,F在线段AA1上.
(1)AF为何值时,CF⊥平面B1DF?
(2)设AF=1,求平面B1CF与平面ABC所成的锐二面角的余弦值.
 [解] (1)因为直三棱柱ABC-A1B1C1中,
[解] (1)因为直三棱柱ABC-A1B1C1中,
BB1⊥面ABC,∠ABC=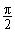 .
.
以B点为原点,BA、BC、BB1分别为x、y、z轴建立如图所示空间直角坐标系.
因为AC=2,∠ABC=90º,所以AB=BC=,
 从而B(0,0,0),A
从而B(0,0,0),A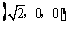 ,C
,C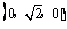 ,B1(0,0,3),A1
,B1(0,0,3),A1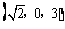 ,C1
,C1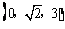 ,D
,D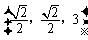 ,E
,E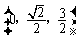 .
.
所以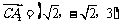 ,
,
设AF=x,则F(,0,x),
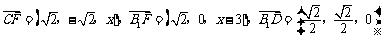 .
.
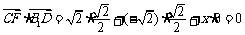 ,所以
,所以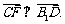
要使CF⊥平面B1DF,只需CF⊥B1F.
由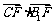 =2+x(x-3)=0,得x=1或x=2,
=2+x(x-3)=0,得x=1或x=2,
故当AF=1或2时,CF⊥平面B1DF.……………… 5分
(2)由(1)知平面ABC的法向量为n1=(0,0,1).
设平面B1CF的法向量为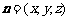 ,则由
,则由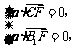 得
得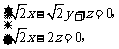
令z=1得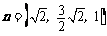 ,
,
所以平面B1CF与平面ABC所成的锐二面角的余弦值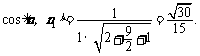
………………… 10分
22.动点P在x轴与直线l:y=3之间的区域(含边界)上运动,且到点F(0,1)和直线l的距离之和为4.
(1)求点P的轨迹C的方程;
(2)过点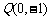 作曲线C的切线,求所作的切线与曲线C所围成区域的面积.
作曲线C的切线,求所作的切线与曲线C所围成区域的面积.
[解](1)设P(x,y),根据题意,得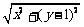 +3-y=4,化简,得y=
+3-y=4,化简,得y=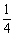 x2(y≤3).
x2(y≤3).
…………………4分
(2)设过Q的直线方程为y=kx-1,代入抛物线方程,整理得x2-4kx+4=0.
由△=16k2-16=0.解得k=±1.
于是所求切线方程为y=±x-1(亦可用导数求得切线方程).
切点的坐标为(2,1),(-2,1).
由对称性知所求的区域的面积为S=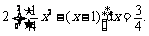 ………………… 10分
………………… 10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com