

3、已知数列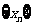 满足
满足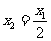 ,
, ,
,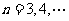 ,若
,若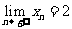 ,则
,则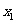 =( )
=( )
A、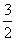 B
B 3 C、4 D、5
3 C、4 D、5
2、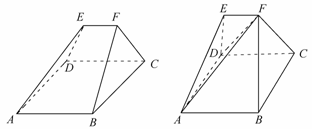 如图(1)所示,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF=
如图(1)所示,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF∥AB,EF=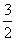 ,EF与面AC的距离为2,则该多面体的体积是( )
,EF与面AC的距离为2,则该多面体的体积是( )
?A.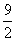 B.5
C.6
D.
B.5
C.6
D.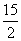
1、设随机变量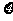 服从正态分布
服从正态分布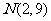 ,若
,若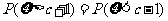 ,则
,则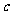 = ( )
= ( )
A.1 B.2 C.3 D.4
10、解:由已知得函数
(1)当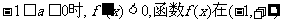 上单调递减。
上单调递减。
(2)当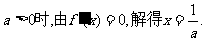
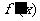 、
、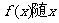 的变化情况如下表:
的变化情况如下表:
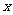 |
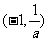 |
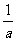 |
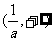 |
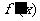 |
- |
0 |
+ |
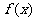 |
 |
极小值 |
 |
从上表可知

9、三角:解: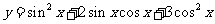
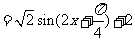
⑴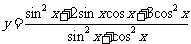
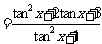
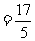 .
.
⑵在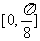 上单调递增,在
上单调递增,在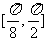 上单调递减.
上单调递减.
所以,当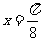 时,
时,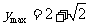 ;当
;当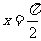 时,
时,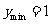 . 故
. 故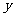 的值域为
的值域为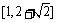 .
.
8、立体:(Ⅰ)由长方体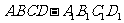 知:
知: ,又
,又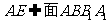 ,所以,
,所以,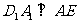 .
.
在矩形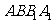 中,
中,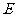 为
为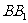 中点且
中点且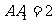 ,
,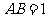 ,所以,
,所以,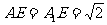 ,所以,
,所以,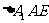 为等腰直角三角形,
为等腰直角三角形,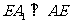 .所以,
.所以,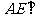 面
面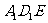 .所以,
.所以,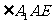 就是直线
就是直线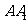 与平面
与平面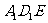 所成的角,为
所成的角,为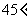 .
.
(Ⅱ) 注意到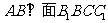 ,所以,面
,所以,面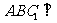
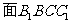 ,所以,只需在
,所以,只需在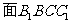 内过点
内过点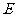 作
作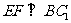 于F,则
于F,则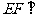 面
面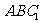 .
.
过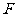 作
作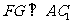 于G,连EG,则
于G,连EG,则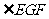 就是二面角
就是二面角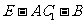 的平面角.
的平面角.
在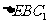 中,
中,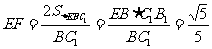 ,所以,
,所以,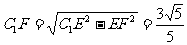 .
.
在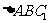 中,
中,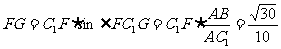 .
.
在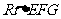 中,
中,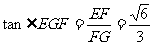 .
.
所以,二面角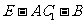 的平面角的大小为
的平面角的大小为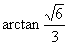 .
.
(Ⅲ)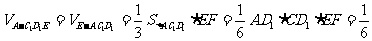 .
.
另一方面,也可以利用等积转化. 因为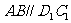 ,所以,
,所以,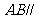
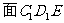 .所以,点A到平
.所以,点A到平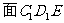 的距离就等于点
的距离就等于点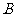 到平
到平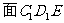 的距离.所以,
的距离.所以,
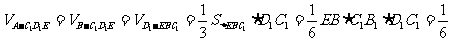 .12分
.12分
7、概率:(Ⅰ)、“飞碟投入红袋”,“飞碟投入蓝袋”,“飞碟不入袋”分别记
为事件A,B,C. 则由题意知: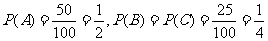
因每次投掷飞碟为相互独立事件,故4次投掷中恰有三次投入红袋的概率为;
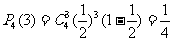
(Ⅱ)、两次投掷得分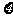 的得分可取值为0,1,2,3,4则:
的得分可取值为0,1,2,3,4则: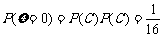
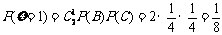
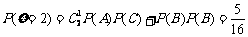
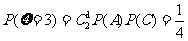 ;
;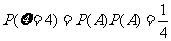

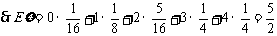
9、已知函数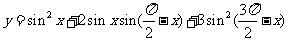 .
.
(1)若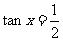 ,求
,求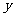 的值;
的值;
(2)若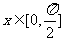 ,求函数单调区间及值域.
,求函数单调区间及值域.
10(13分)设函数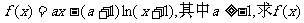 的单调区间.
的单调区间.
8、(本题满分14分)长方体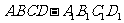 中,
中,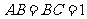 ,
,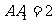 ,
,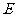 是侧棱
是侧棱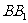 中点.
中点.
 (Ⅰ)求直线
(Ⅰ)求直线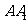 与平面
与平面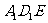 所成角的大小;
所成角的大小;
(Ⅱ)求二面角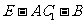 的大小;
的大小;
(Ⅲ)求三棱锥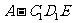 的体积.
的体积.
7、(本题满分12分)投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.现知某人在以前投掷1000次的试验中,有500次入红袋,250次入蓝袋,其余不能入袋
(Ⅰ)求该人在4次投掷中恰有三次投入红袋的概率;
(Ⅱ) 求该人两次投掷后得分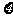 的数学期望.
的数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com