
5、[解析]设△OAB的边长为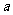 ,则不妨设
,则不妨设 ,代入
,代入 ,得
,得 ;同理,设△OCD的边长为
;同理,设△OCD的边长为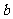 ,可得
,可得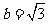 .
. ,
, .
.
4、[解析]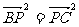 ,即
,即 ,
, ,
,
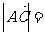
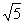 ,故选C.
,故选C.
3、[解析]由条件 有
有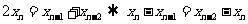 ,∴
,∴
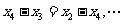
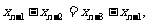
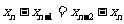 ,累加得
,累加得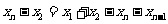 ,代入
,代入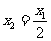 得
得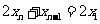 ,两边同取极限得,
,两边同取极限得,
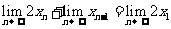 ,即
,即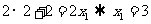 ,选B
,选B
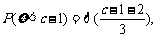

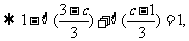 解得
解得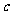 =2, 所以选B.
=2, 所以选B.
2、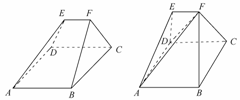 [解析]用特殊图形.如图(2)所示,使ED⊥平面ABCD,且使ED=2.连AF、DF.则EF⊥面ADE.
[解析]用特殊图形.如图(2)所示,使ED⊥平面ABCD,且使ED=2.连AF、DF.则EF⊥面ADE.
∵VF-ADE=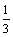 ·EF·S△ADE=
·EF·S△ADE=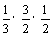 ×3×2=
×3×2=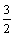 .
.
VF-ABCD=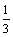 ·DE·S□ABCD=
·DE·S□ABCD=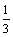 ·2·32=6.∴V多面体=
·2·32=6.∴V多面体=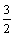 +6=
+6=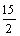 .选D.
.选D.
10、设直线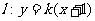 与椭圆
与椭圆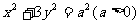 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(I)证明: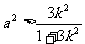
(II)若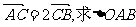 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
9、如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
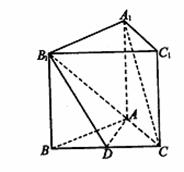 (I)求证:A1C//平面AB1D;
(I)求证:A1C//平面AB1D;
(II)求二面角B-AB1-D的大小;
(III)求点C到平面AB1D的距离.
8、已知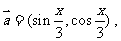
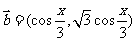 ,函数
,函数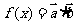 .
.
(1)将f(x)写成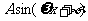 的形式,并求其图象对称中心的坐标;
的形式,并求其图象对称中心的坐标;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
7、同时抛掷15枚均匀的硬币一次.(1)试求至多有1枚正面向上的概率;
(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.
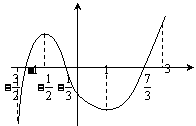
6、已知函数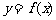 在定义域
在定义域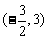 上可导,其图像如图,记
上可导,其图像如图,记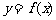 的导函数
的导函数 ,则不等式
,则不等式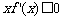 的解集是________.
的解集是________.
4、三角形ABC中AP为BC边上的中线,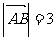 ,
,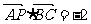 ,则
,则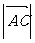 =
=
 5、O为坐标原点,正△OAB中A、B在抛物线
5、O为坐标原点,正△OAB中A、B在抛物线 上,正△OCD中C、D在抛物线
上,正△OCD中C、D在抛物线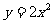 上,则△ OAB与△OCD的面积之比为
.
上,则△ OAB与△OCD的面积之比为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com