
10、设定义在 上的函数
上的函数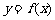 的图象为C,C的端点为点A、B,M是C上的任意一点,向量
的图象为C,C的端点为点A、B,M是C上的任意一点,向量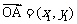 ,
, ,
,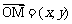 ,若
,若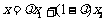 ,记向量
,记向量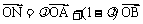 .现在定义“函数
.现在定义“函数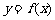 在
在 上可在标准k下线性近似”是指
上可在标准k下线性近似”是指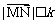 恒成立,其中k是一个人为确定的正数.
恒成立,其中k是一个人为确定的正数.
(1)证明: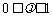 ;
;
(2)请你给出一个标准k的范围,使得[0,1]上的函数y=x2与y=x3中有且只有一个可在标准k下线性近似.
9、甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.
(1)求甲答对试题数ξ的概率分布及数学期望;
(2)求甲、乙两人至少有一人考试合格的概率.
7、已知数列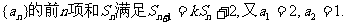
(1)求k的值及通项公式an.
(2)求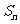 .
.
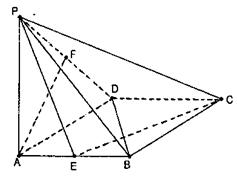 8、如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=AB=2,E,F分别是AB与PD的中点.
8、如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=AB=2,E,F分别是AB与PD的中点.
(1)求证:PC⊥BD;
(2)求证:AF//平面PEC;
(3)求二面角P-EC-D的大小.
6、己知:函数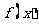 满足
满足 ,又
,又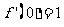 .则函数
.则函数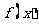 的解析式为
的解析式为

5、已知单位正方体ABCD-A1B1C1D1对棱BB1,DD1上有两个动点E、F,BE=D1F,设EF与面AB1所成角为α,与面BC1所成角为β,则α+β的最大值为 .
4、f(x)是定义在(0,+∞)上的非负可导函数,且满足xf‘(x)-f(x)>0,对任意正数a、b,若a<b,则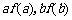 的大小关系为
.
的大小关系为
.
3、若函数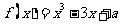 有3个不同的零点,则实数
有3个不同的零点,则实数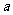 的取值范围是 ( )答A
的取值范围是 ( )答A
A.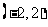 B.
B. 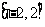 C.
C.  D.
D.
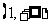
1、已知△ABC的三个顶点A、B、C及平面内一点P满足: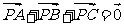 ,若实数
,若实数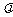 满足:
满足: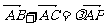 ,则
,则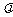 的值为 ( )答C
的值为 ( )答C
A.2
B.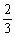 C.3 D.6
C.3 D.6
2、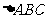 中,若
中,若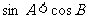 ,则
,则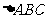 为 ( )答C
为 ( )答C
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
10、解法一: (Ⅰ)在直三棱柱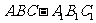 中,
中,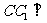 底面
底面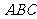 ,
,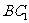 在底面上的射影为
在底面上的射影为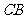 .
.
由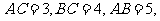 可得
可得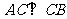 .,所以
.,所以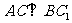 .
.
(Ⅱ)过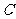 作
作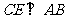 于
于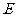 ,连结
,连结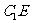 .
.
 由
由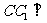 底面
底面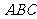 可得
可得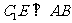 .
.
故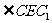 为二面角
为二面角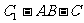 的平面角.
的平面角.
在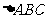 中,
中,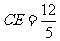 ,在Rt
,在Rt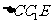 中,
中,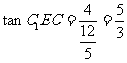 ,
,
故所求二面角的大小为 .
.
(Ⅲ)存在点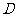 使
使 ∥平面
∥平面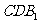 ,且
,且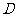 为
为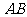 中点,下面给出证明.
中点,下面给出证明.
设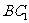 与
与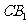 交于点
交于点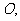 则
则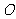 为
为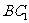 中点.在
中点.在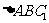 中, 连结
中, 连结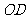 ,
,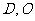 分别为
分别为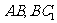 的中点,故
的中点,故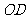 为
为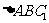 的中位线,
的中位线,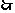
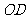 ∥
∥ ,又
,又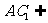 平面
平面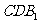 ,
,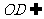 平面
平面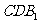 ,
,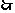
 ∥平面
∥平面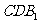 .故存在点
.故存在点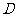 为
为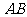 中点,使
中点,使 ∥平面
∥平面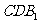 .
.
解法二
 直三棱柱
直三棱柱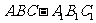 ,底面三边长
,底面三边长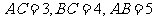 ,
,
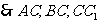 两两垂直.如图以
两两垂直.如图以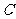 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系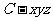 ,则
,则
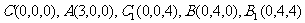 .
.
(Ⅰ)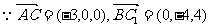 ,
,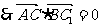 ,故
,故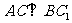 .
.
 (Ⅱ)平面
(Ⅱ)平面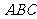 的一个法向量为
的一个法向量为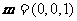 ,
,
设平面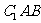 的一个法向量为
的一个法向量为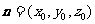 ,
,
 ,
,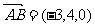 ,
,
由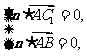 得
得
令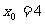 ,则
,则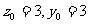 .则
.则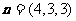 .
.
故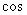 <
< >=
>=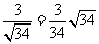 .所求二面角的大小为
.所求二面角的大小为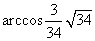 。 (Ⅲ)同解法一
。 (Ⅲ)同解法一
 21世纪教育网
21世纪教育网
9、解:(I)由题意得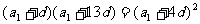 ,
,
整理得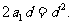
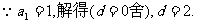
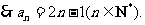
(II)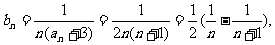
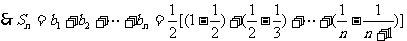
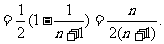 假设存在整数
假设存在整数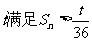 总成立。
总成立。
又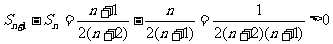 ,
,
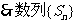 是单调递增的。
是单调递增的。
又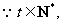
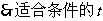 的最大值为8。
的最大值为8。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com