
3、关于函数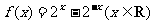 有下列三个结论:①
有下列三个结论:①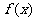 的值域为R;②
的值域为R;②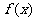 是R上的增函数;③对任意
是R上的增函数;③对任意 成立;其中所有正确的序号为( )答D
成立;其中所有正确的序号为( )答D
A.①② B.①③ C.②③ D.①②③
2、在正n棱锥中,相邻两侧面所成二面角的平面角的取值范围是( )
A、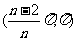 B、
B、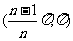 C、
C、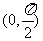 D、
D、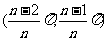
1、已知函数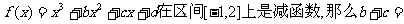 ( )答B
( )答B
A.有最大值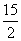 B.有最大值-
B.有最大值-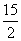 C.有最小值
C.有最小值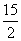 D.有最小值-
D.有最小值-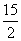
10、[解答](1)由题意,x1≤x≤x2,即x1≤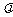 x1+(1-
x1+(1-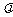 )x2≤x2,∴ x1- x2≤(x1-x2)
)x2≤x2,∴ x1- x2≤(x1-x2)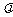 ≤0.
≤0.
∵ x1- x2<0,∴ 0≤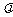 ≤1.
≤1.
(2)由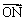 =
=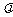
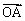 +(1-
+(1-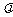 )
)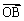 ,得
,得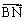 =
=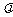
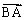 .
.
所以B、N、A三点在一条直线上.
又由(1)的结论,N在线段AB上,且与点M的横坐标相同.
对于 [0,1]上的函数y=x2,A(0,0),B(1,1),
则有|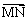 |= x -x2 =
|= x -x2 =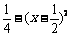 ,故
,故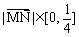 .
.
对于[0,1]上的函数y=x3,则有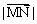 = x-x3= g(x).
= x-x3= g(x).
在(0,1)上, g′(x)= 1-3 x2,
可知在(0,1)上y=
g(x)只有一个极大值点x=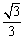 ,
,
所以函数y= g(x)在(0,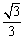 )上是增函数;在(
)上是增函数;在(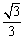 ,1)上是减函数.
,1)上是减函数.
又g(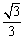 )=
)=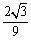 ,故
,故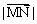
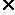 [0,
[0,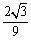 ].
].
经过比较,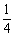 <
<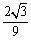 ,所以取k
,所以取k [
[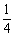 ,
,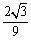 ),则有函数y=x2在[0,1]上可在标准k下线性近似,函数y=x3在[0,1]上不可在标准k下线性近似.
),则有函数y=x2在[0,1]上可在标准k下线性近似,函数y=x3在[0,1]上不可在标准k下线性近似.
9、[解答] (1)依题意,甲答对试题数ξ的概率分布如下:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
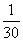 |
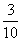 |
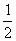 |
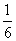 |
甲答对试题数ξ的数学期望.
Eξ=0×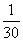 +1×
+1×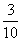 +2×
+2×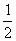 +3×
+3×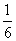 =
=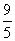
(2)设甲、乙两人考试合格的事件分别为A、B,则
P(A)=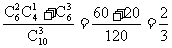 P(B)=
P(B)=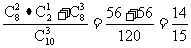
因为事件A、B相互独立,
方法一:∴甲、乙两人考试均不合格的概率为
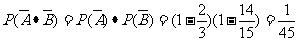
∴甲、乙两人至少有一人考试合格的概率P=1-P(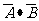 )=1-
)=1-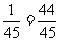
方法二:∴甲、乙两人至少有一人考试合格的概率为
P=P(A·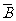 )+P(
)+P(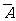 ·B)+P(A·B)=P(A)P(
·B)+P(A·B)=P(A)P(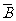 )+P(
)+P(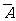 )·
)·
P(B)+P(A)P(B)=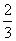 ×
×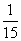 +
+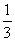 ×
×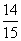 +
+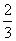 ×
×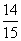 =
=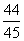
8、[解答]:(I)连结AC,则AC⊥BD。∵PA⊥平面ABCD,AC是斜线PC在平面ABCD上的射影,∴由三垂线定理得PC⊥BD。
(II)取PC的中点K,连结FK、EK, 则四边形AEKF是平行四边形。
∴AF//EK,又EK 平面PEC,AF
平面PEC,AF 平面PEC,∴AF//平面PEC。
平面PEC,∴AF//平面PEC。
(III)延长DA、CE交于M,过A作AH⊥CM于H,
连结PH,由于PA⊥平面ABCD,可得PH⊥CM。
∴∠PHA为所求二面角P-EC-D的平面角。∵E为AB的中点,AE//CD,∴AM=AD=2,
在△AME中,∠MAE=120°,
由余弦定理得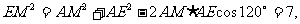
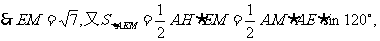
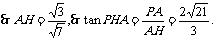
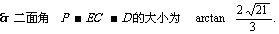
7、[解答](1)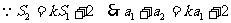 ,又
,又 (2)由(1)
(2)由(1)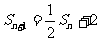 ① 当
① 当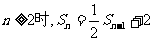 ②
②
①-②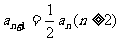
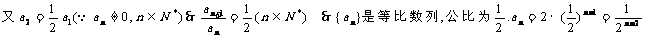

6、[解析]由已知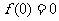 ,当
,当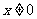 时,原方程化为
时,原方程化为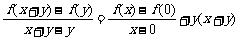 .由等式右边存在极限,
.由等式右边存在极限,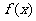 处处可导.对原方程两边令
处处可导.对原方程两边令 ,得
,得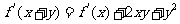 .
.
令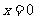 ,
,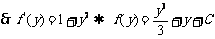 (
(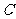 为常数).又
为常数).又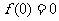 ,得
,得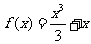 .
.
5、[解析]由对称性可知α=β,又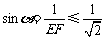 ,所以α≤45°,α+β≤90°.
,所以α≤45°,α+β≤90°.
4、[解析]设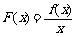 ,则
,则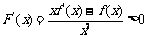 ,故
,故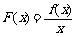 为增函数,由a<b,有
为增函数,由a<b,有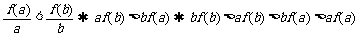
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com