
8、解:(1)∵点A、D分别是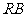 、
、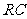 的中点,∴
的中点,∴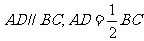 .
.
 ∴∠
∴∠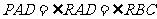 =90º.∴
=90º.∴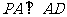 .∴
.∴ 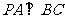 ,
,
∵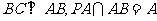 ,∴
,∴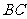 ⊥平面
⊥平面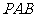 .
.
∵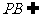 平面
平面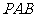 ,∴
,∴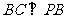 .
.
(2)法1:取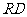 的中点
的中点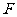 ,连结
,连结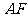 、
、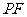 . ∵
. ∵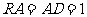 ,∴
,∴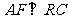 ∵
∵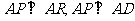 , ∴
, ∴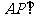 平面
平面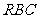 .
.
∵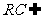 平面
平面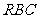 ,∴
,∴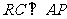 . ∵
. ∵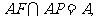 ∴
∴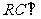 平面
平面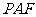 .
.
∵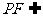 平面
平面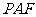 , ∴
, ∴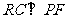 .
.
∴∠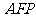 是二面角
是二面角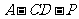 的平面角. 在Rt△
的平面角. 在Rt△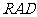 中,
中, 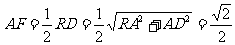 ,
,
在Rt△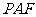 中,
中, 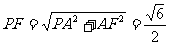 ,
,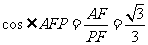 .
.
 ∴ 二面角
∴ 二面角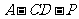 的平面角的余弦值是
的平面角的余弦值是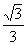

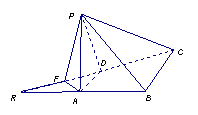
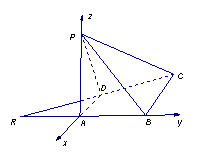
法2:建立如图所示的空间直角坐标系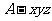 .
.
则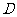 (-1,0,0),
(-1,0,0),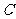 (-2,1,0),
(-2,1,0),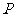 (0,0,1).
(0,0,1).
∴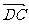 =(-1,1,0),
=(-1,1,0),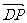 =(1,0,1),
设平面
=(1,0,1),
设平面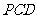 的法向量为
的法向量为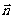 =(x,y,z),则:
=(x,y,z),则:
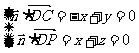 , 令
, 令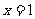 ,得
,得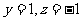 ,∴
,∴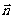 =(1,1,-1).
=(1,1,-1).
显然,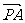 是平面
是平面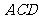 的一个法向量,
的一个法向量,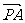 =(
=(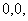
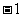 ).
).
∴cos<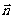 ,
,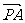 >=
>=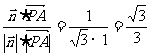 . ∴二面角
. ∴二面角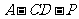 的平面角的余弦值是
的平面角的余弦值是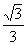 .
.
7、[解析](Ⅰ)由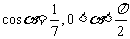 ,得
,得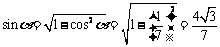
∴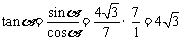 ,于是
,于是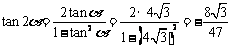
(Ⅱ)由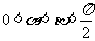 ,得
,得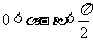 又∵
又∵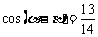 ,∴
,∴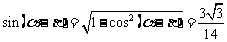
由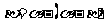 得:
得: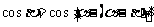
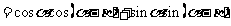
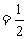
所以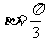
1、答B 2、[解析]进行极限分析,当顶点无限趋近于底面正多边形的中心时,相邻两侧面所成二面角 ,且
,且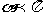 ;当锥体
;当锥体 且底面正多边形相对固定不变时,正n棱锥形状趋近于正n棱柱,
且底面正多边形相对固定不变时,正n棱锥形状趋近于正n棱柱,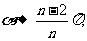 且
且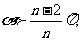 选A 3、[解析]D 4、[解析]设
选A 3、[解析]D 4、[解析]设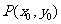 ,由
,由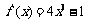 ,得
,得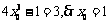 ,从而
,从而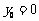 .
.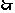 点P的坐标为(1,0).5、答26 6、[解析]设
点P的坐标为(1,0).5、答26 6、[解析]设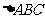 的外接圆的半径为
的外接圆的半径为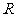 ,
,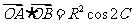 ,
,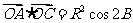 ,
, 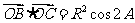 .
.
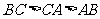
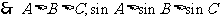
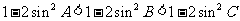
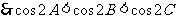
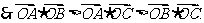
10、已知定义域为R的二次函数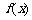 的最小值为0且有
的最小值为0且有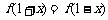 ,直线
,直线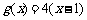 被
被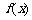 的图像截得的弦长为
的图像截得的弦长为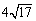 ,数列
,数列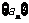 满足
满足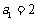 ,
,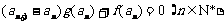 .
.
(1)函数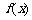 ;
;
(2)求数列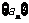 的通项公式;
的通项公式;
(3)设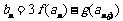 ,求数列
,求数列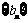 的最值及相应的n.
的最值及相应的n.
9、一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
(1)求这箱产品被用户接收的概率;
(2)记抽检的产品件数为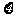 ,求
,求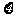 的分布列和数学期望.
的分布列和数学期望.
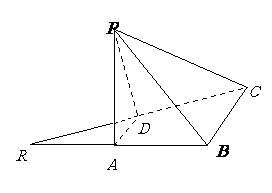
8、如图,已知等腰直角三角形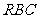 ,其中∠
,其中∠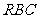 =90º,
=90º,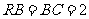 .
.
点A、D分别是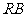 、
、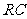 的中点,现将△
的中点,现将△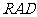 沿着边
沿着边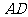 折起到△
折起到△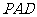 位置,
位置,
 使
使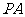 ⊥
⊥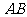 ,连结
,连结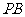 、
、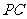 .
.
(1)求证: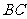 ⊥
⊥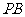 ;
;
(2)求二面角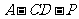 的平面角的余弦值.
的平面角的余弦值.
7、已知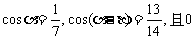 <
<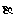 <
< <
<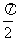 ,
,
(Ⅰ)求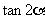 的值.
的值.
(Ⅱ)求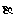 .
.
6、已知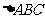 的外接圆的圆心
的外接圆的圆心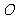 ,
,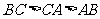 ,则
,则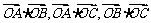 的大小关系为______.
的大小关系为______.
5、已知双曲线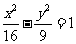 的左、右焦点分别为
的左、右焦点分别为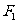 ,
,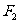 ,过
,过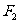 的直线与该双曲线的右支交于
的直线与该双曲线的右支交于 、
、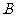 两点,若
两点,若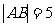 ,则
,则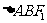 的周长为_________.
的周长为_________.
4、若曲线 在点P处的切线平行于直线3x-y=0,则点P的坐标为
.
在点P处的切线平行于直线3x-y=0,则点P的坐标为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com