

1、以下函数f (x),具有性质(x-1) f ¢(x)≥0从而有f (0)+ f (2) ≥ 2 f (1)的函数是( )
A. f(x)= (x-1)3 B. f(x)= (x-1)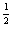 C. f(x)= (x-1)
C. f(x)= (x-1)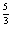 D. f(x)= (x-1)
D. f(x)= (x-1)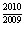
10、(1)
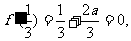
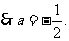
(2)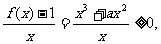
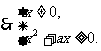
当 当
当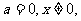 当
当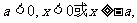
 21世纪教育网
21世纪教育网
9、[解答](1) 各道题答对与否互不影响,是独立事件:
.  =0.192.
=0.192.
(2) “至多答对4道题”与“5道题全答对”是对立事件, 即
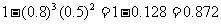
(3)
依题意: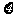 =40、60、80、100.
=40、60、80、100.
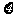 |
40 |
60 |
80 |
100 |
|
P |
0.008 |
0.096 |
0.384 |
0.512 |
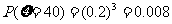 ;
;
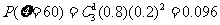
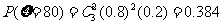 ;
; 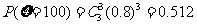
因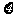 满足二项分布,故
满足二项分布,故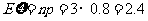
8、[解答](1)取CD中点E,连结EF,BE. ∵F是PC中点,∴EF//PD.
∵EF 平面PAD,PD
平面PAD,PD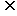 平面PAD,∴EF//平面PAD.
平面PAD,∴EF//平面PAD.
∵AB = CD,AB//CD,∴DEAB,∴BE//AD.
∵BE 平面PAD,AD
平面PAD,AD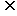 平面PAD,∴BE//平面PAD.
平面PAD,∴BE//平面PAD.
∵EF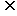 平面BEF,BE
平面BEF,BE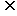 平面BEF,EF∩BE = E,∴平面BEF//平面PAD.
平面BEF,EF∩BE = E,∴平面BEF//平面PAD.
而BF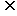 平面BEF,∴BF//平面PAD.
平面BEF,∴BF//平面PAD.
(2)当λ = 1,即F为PC中点时有BF⊥CD.
∵PA⊥平面ABCD,CD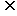 平面ABCD,∴PA⊥CD.
平面ABCD,∴PA⊥CD.
∵∠A = 90°,AB//CD,∴CD⊥AD.
∵PA 平面PAD,AD
平面PAD,AD 平面PAD,PA∩AD = A,
平面PAD,PA∩AD = A,
∴CD⊥平面PAD.
由(1)知平面PAD//平面BEF,∴CD⊥平面BEF.
∵BF 平面BEF,∴CD⊥BF.
平面BEF,∴CD⊥BF.
7、[解答](I)由题意及正弦定理,得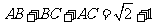 ,
,
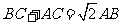 ,两式相减,得
,两式相减,得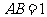 .
.
(II)由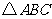 的面积
的面积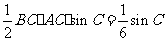 ,得
,得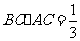 ,
,
由余弦定理,得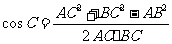
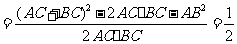 ,
,
所以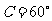 .
.
5、[解答](- ∞,- 1)∪(1,+∞) 6、[解答]20
4、[解答]若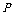 和
和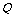 都正确,则由
都正确,则由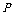 ,有
,有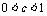 .由
.由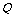 ,有
,有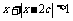 的解集为
的解集为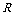 .
.
用函数认识不等式,只需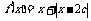 的最小值
的最小值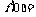 2
2 此时
此时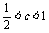 .
.
若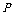 和
和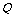 都不正确,则由
都不正确,则由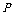 ,有
,有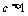 .由
.由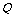 ,有
,有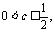 其交集为空集,此时
其交集为空集,此时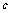 不存在.
不存在.
由题设知,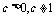 ,用补集思想,所求
,用补集思想,所求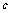 的取值范围为
的取值范围为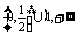
3、[解答]A
2、[解答] 设F(x)= f (x)g(x), 当x<0时,∵F′(x)= f′(x)g(x)+f (x)g′(x)>0.
∴F(x)在R上为增函数.
 ∵F(-x)= f (-x)g (-x)=-f (x)·g (x).=-F(x).
∵F(-x)= f (-x)g (-x)=-f (x)·g (x).=-F(x).
故F(x)为(-∞,0)∪(0,+∞)上的奇函数.
∴F(x)在R 上亦为增函数.
上亦为增函数.
已知g(-3)=0,必有F(-3)=F(3)=0.
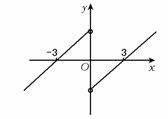
构造如图的F(x)的图象,可知
F(x)<0的解集为x∈(-∞,-3)∪(0,3).
1、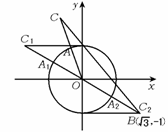 [解答] 如图,点A(cosθ,sinθ)在圆
[解答] 如图,点A(cosθ,sinθ)在圆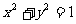 上运动时,延OA到C,使
上运动时,延OA到C,使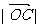 =
=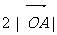 =2a, 求
=2a, 求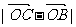 的最值,显然
的最值,显然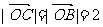 .当
.当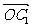 与
与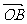
反向时有最大值4, 与
与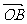 同向时有最小值0. ∴选D.
同向时有最小值0. ∴选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com