
 4、若直线y=2a与函数y=|ax-1|(a>0,a≠1)的图象有两个公共点,则a的取值范围是
.
4、若直线y=2a与函数y=|ax-1|(a>0,a≠1)的图象有两个公共点,则a的取值范围是
.
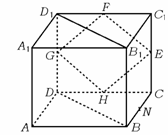
5、 如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F、G、H分别是棱CC1,C1D1,D1,D的中点,N是BC中点,点M在四边形EFGH及其内部运动,则M只要满足
条件 时,就有MN∥平面B1BDD1(请填上你认为正确的一个条件即可,不必考虑全部可能情况).
3、若集合A1,A2满足A1∪A2=A,则称(A1,A2)为集合A的一种分拆,并规定:当且仅当A1=A2时,(A1,A2)与(A2,A1)为集合A的同一种分拆,则集合A={a1,a2,a3}的不同分拆种数是( )A?
?A?27
B ?26
C?9
D?8?
?26
C?9
D?8?
2、若{an}是等差数列,首项a1>0,a2003+a2004>0,a2003·a2004<0,则使前n项和Sn>0成立的最大自然数n是 ( )B
?A.4005 B.4006 C.4007 D.4008?
1、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是 ( )B
?A.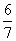 B.
B.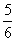 C.
C.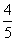 D.
D. ?
?
10、[解答]由Sn+1 = 3Sn + 2n+1可得:bn+1 = 3bn + 2n ∴bn+1+ 2n+1 = 3 (bn + 2n)∴{ bn + 2n }为等比数列
∴bn + 2n = (b1 + 2)·3n–1 ∴bn = 3n – 2n
(2)∵1 + 21 + 22 + …+ 27 = 28 – 1 = 255.∴a260是第9行中的第5个数
设公差为d,则a260 = a256 + 4d.又∵a256 = b9 ∴a260 = b9+ 4d.∴18771 = (39 – 29) + 4d ∴d = –100
又∵第k行中的数列的首项为bk,公差为d,项数为2k–1.
∴Sk = 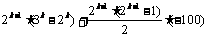 =
=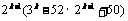
9、[解答](1)f (x) = 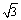 sin
(
sin
(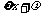 ) –
cos (
) –
cos (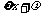 )
= 2sin (
)
= 2sin (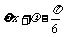 )
)
由f (–x) = f (x)可得sin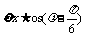 =
0 ∴
=
0 ∴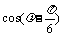 = 0 ∴
= 0 ∴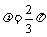
又∵f (x) = f (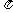 –x)
∴f (
–x)
∴f (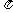 –x) = f
(–x) ∴周期T =
–x) = f
(–x) ∴周期T = 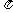 ∴
∴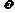 = 2 ∵f (x) = 2cos 2x ∴f (
= 2 ∵f (x) = 2cos 2x ∴f (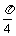 )
= 0
)
= 0
(2)g (x) = f (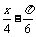 )
= 2cos2 (
)
= 2cos2 (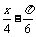 ) =
2cos(
) =
2cos(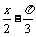 ) ∴
) ∴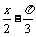 = k
= k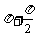 ∴x = 2 k
∴x = 2 k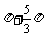
∴对称中心为(2 k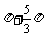 ,0)k∈Z
,0)k∈Z
8、[思考] 本题的实质是检查3个灯泡,可视为3次独立重复试验.(1)中3个灯泡在使用1000小时之后恰坏1个,相当于在3次独立重复试验中事件A恰好发生2次(事件A是“灯泡的使用时数在1000小时以上”);(2)中指“恰好坏1个”与“3个都未坏”这两种情况,即事件A发生2次和发生3次,可用独立重复试验的方法求解.
[解答] 设“灯泡的使用时数在1000小时以上”为事件A,则P(A)=0.7,检查3个灯泡可视为3次独立重复试验.
(1)3个灯泡在使用1000小时之后恰好坏1个,相当于在3次独立重复试验中事件A恰好发生2次.
∴P3(2) =C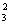 (0.7)2(1-0.7)3-2=3×0.49×0.3=0.441.
(0.7)2(1-0.7)3-2=3×0.49×0.3=0.441.
(2)“3个灯泡在使用1000小时之后最多只坏1个”包括了“恰好坏1个”和“3个都未坏”这两种情况,它们彼此互斥,相当于A发生2次和发生3次的概率和,即所求概率为P3(2)+P3(3)=0.441+C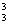 0.73=0.784.
0.73=0.784.
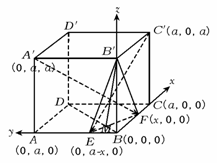
7、[解答](1)如图,以B为原点,直线BC,BA,BB′分别为x,y,z轴建立空间直角坐标系,并设 =x,则有:A′(0,a,a),C′(a,0,a). E(0,a-x,0),F(x,0,0),∴
=x,则有:A′(0,a,a),C′(a,0,a). E(0,a-x,0),F(x,0,0),∴ =(x,-a,-a),
=(x,-a,-a), =(-a,a-x,-a).
=(-a,a-x,-a).
 ∵
∵ ·
· =(x,-a,-a)(-a,a-x,-a)=-ax-a2+ax+a2=0,
=(x,-a,-a)(-a,a-x,-a)=-ax-a2+ax+a2=0,
∴? ⊥
⊥ .
.
(2)VB′-BEF?= S△EEF·|
S△EEF·|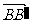 |=
|=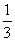 ·
·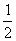 (a-x)·x·a
(a-x)·x·a
=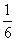 a(a-x)·x≤
a(a-x)·x≤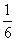 a·
a·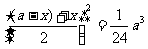 ,
,
当且仅当a-x=a,即x=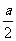 时,
时,
(VB′-BEF)max =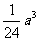 ,
,
此时E、F分别为AB,BC的中点,必EF⊥BD.设垂足为M,连B′M,∵BB′⊥平面ABCD,
由三垂线定理知B′M⊥EF,∠BMB′是二面角B′-EF-B的平面角,
设为θ,∵|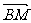 |=
|=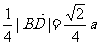 ∴?tanθ=
∴?tanθ=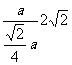 .
.
即θ=arctan2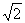 ,则二面角B′-EF-B的大小为arctan2
,则二面角B′-EF-B的大小为arctan2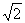 .
.
6、[解答] 与
与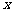 轴正半轴的夹角的取值范围应在向量
轴正半轴的夹角的取值范围应在向量 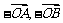 与
与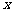 轴正半轴的夹角之间,故
轴正半轴的夹角之间,故 与
与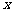 轴正半轴的夹角的取值范围是
轴正半轴的夹角的取值范围是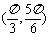 .
.
5、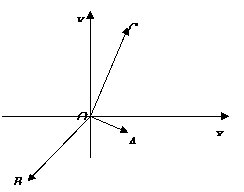 [解答]
[解答]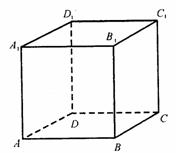 依题意可构造正方体AC1,如图1,在正方体中逐一判断各命题易得正确命题的是②⑤。
依题意可构造正方体AC1,如图1,在正方体中逐一判断各命题易得正确命题的是②⑤。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com