5、[解答]显然HN∥BD，即得HN∥平面B₁BDD₁，为使点M在平面EFGH内运动时总有B₁BDD₁∥M，只需过HN作平面，使之平行于平面B₁BDD₁，将线面平行的问题转化为面面平行的问题.

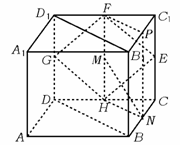　 证：连FH，当点M在HF上运动时，恒有MN∥平面B₁BDD₁

证明如下：连NH，HF，BD，B₁D₁，且平面NHF交B₁C₁于P.　 则NH∥BD，HF∥BB₁，故平面PNHF∥平面B₁BDD₁.　 MN平面PNHF，∴MN∥平面B₁BDD₁.

4、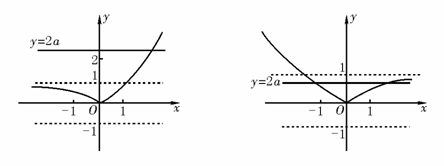[解答]函数y=|a^x-1|=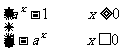，其图象由y=|a^x|(a>0，a≠1)的图象下移一个单位得到.如图，当a>1时，直线y=2a与y=|a^x-1|(a>0，a≠1)的图象仅一个交点； 当0<a<1时，当且仅当0<2a<1时，直线y=2a与y=|a^x-1|(a>0，a≠1)的图象有两个公共点，解得a∈(0，)

3、[解答]由于A={a₁，a₂，a₃}=A₁∪A₂，以A₁为标准分类.

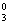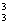A₁是，则A₂={a₁，a₂，a₃}，这种分拆仅一种，即?C·C=1;

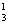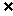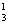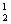如A₁为单元素集，有C种可能,对其中每一种，例如A₁={a₁}，由于必有a₁，a₃∈A₂，且a₁∈A₂或a₁A₂都符合条件.　 这种分拆有?C·C=6种.

如A₁为双元素集，有C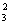种可能,对其中每一种，不妨设A₁={a₁，a₂}，则必a₃∈A₂，此外对a₁，a₂可以不选，选1个或全选，有2²=4种选法，这种分拆共有?C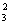·4=12种.

若A₁为三元素集，则A₂可以是{a₁，a₂，a₃}的任何一个子集，故这种分拆有2³种.　 于是共有1+6+12+8=27种不同的分拆.

2、[解答]∵a₁>0，a₂₀₀₃+a₂₀₀₄>0，a₂₀₀₃·a₂₀₀₄<0，且{a_n}为等差数列.

∴{a_n}表示首项为正数，公差为负数的单调递减等差数列，且a₂₀₀₃是绝对值最小的正数，a₂₀₀₄?是绝对值最大的负数(第一个负数)，且|a₂₀₀₃|>|a₂₀₀₄|,

∵在等差数列{a_n}中，a₂₀₀₃+a₂₀₀₄=a₁+a₄₀₀₆>0，S₄₀₀₆=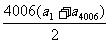>0.

∴使S_n>0成立的最大自然数n是4006.

1、[解答]设每个三棱锥的体积为V′，则剩下的凸多面体的体积是V=1-8，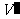

V′=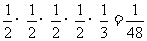　　 ∴V=1-8V′=1-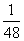×8=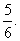

10、已知函数.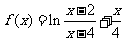

⑴求函数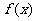的定义域和极值;

⑵若函数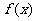在区间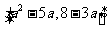上为增函数,求实数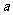的取值范围.

⑶函数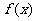的图象是否为中心对称图形?若是请指出对称中心,并证明;若不是,请说明理由.

9、已知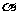为第二象限的角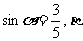，为第三象限的角，.

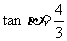　 (I)求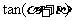的值.

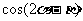　 (II)求的值.

8、校明星篮球队就要组建了，需要在各班选拔预备队员，规定投篮成绩A级的可作为入围选手.选拔过程中每人最多投篮5次，若投中了3次则确定为B级，若投中4次以上则可确定为A级，已知高三(1)班阿明每次投篮投中的概率是.

(1)求阿明投篮4次才被确定为B级的概率；

(2)若连续两次投篮不中则停止投篮，求阿明不能入围的概率.

7、如图所示，已知在矩形ABCD中，AB=1，BC=a(a>0)，PA⊥平面AC，且PA=1.

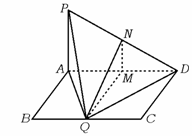(1)问BC边上是否存在Q，便得PQ⊥QD，并说明理由；(2)若BC边上有且只有一点Q，使得PQ⊥QD，

求这时二面角Q-PD-A的大小

6、在袋里装30个小球，其彩球中有n(n≥2)个红球，5个蓝球，10个黄球，其余为白球.若从袋里取出3个都是相同颜色的彩球(无白色)的概率是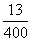，红球的个数　　　 ，从袋中任取3个小球至少有一个是红球的概率是　　　 。

.