
3.两个计数原理的区别:
如果完成一件事,有n类办法,不论哪一类办法中的哪一种方法,都能独立完成这件事,用分类计数原理,
如果完成一件事需要分成几个步骤,各步骤都不可缺少,需要完成所有步骤才能完成这件事,是分步问题,用分步计数原理.
两个计数原理用来计算完成一件事的不同方法种数的,是计算排列组合,概率统计的基础,在生产,生活及科学实验中有广泛的应用.
2.分步计数原理:做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有N=m1×m2×……mn 种不同的方法
1.分类计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法 那么完成这件事共有
那么完成这件事共有
N=m1+m2+……+mn 种不同的方法
2.理解排列的意义;掌握排列数计算公式,并能用它解决一些简单的应用问题.
1.掌握分类计数原理与分步计数原理,并能用它们分析和解决一些简单的应用问题;
10、[解答]解: ⑴函数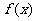 的定义域为(-∞,2)∪(4,+∞),由
的定义域为(-∞,2)∪(4,+∞),由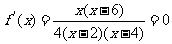 得:
得: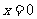 或
或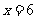 ,所以
,所以
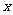 |
(-∞,0) |
0 |
(0,2) |
(4,6) |
6 |
(6,+∞) |
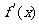 |
+ |
0 |
- |
- |
0 |
+ |
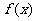 |
↗ |
极大值 |
↘ |
↘ |
极小值 |
↗ |
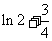
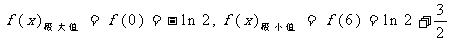
⑵由⑴知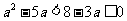 或
或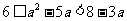 所以
所以 或
或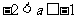
⑶由⑴知函数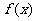 的图象若是中心对称图形,则中心一定在两极值点的中心(3,
的图象若是中心对称图形,则中心一定在两极值点的中心(3, 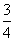 ),
),
下面证明:设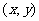 是函数
是函数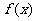 的图象上的任意一点,则
的图象上的任意一点,则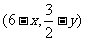 是它关于(3,
是它关于(3, 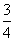 )的对称点,而
)的对称点,而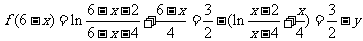 ,即
,即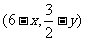 也在函数
也在函数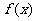 的图象上.所以函数
的图象上.所以函数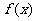 的图象是中心对称图形,其中心是(3,
的图象是中心对称图形,其中心是(3, 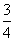 )
)
9、[解答](I)解:因为α为第二象限的角,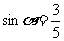 ,所以,
,所以,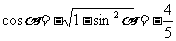 ,
,
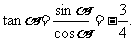 又
又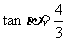 ,所以,
,所以,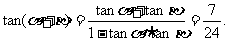
(II)解:因为β为第三象限的角,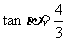 ,所以,
,所以,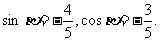
又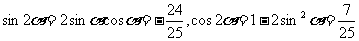 ,
,
所以,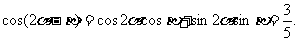
8、[解答](1)求阿明投篮4次才被确定为B级的概率,即求前3次中恰有2次投中且第4次必投中的概率,其概率为P=C23·( )2·
)2· ·
· =
=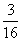 .
.
(2)若连续两次投篮不中则停止投篮,阿明不能入围,该事件可分为下列几类:
①5次投中3次,有C24种可能投球方式,其概率为:P(3)=C24·( )5=
)5=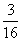 ;
;
②投中2次,其分别有“中中否否”、“中否中否否”、“否中中否否”、“否中否中否”4类投球方式,其概率为:P(2)=( )4+3·(
)4+3·( )5=
)5=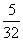 ;
;
③投中1次,其分别有“中否否”、“否中否否”2类投球方式,
其概率为:P(1)=( )3+(
)3+( )4=
)4=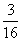 ;
;
④投中0次,其仅有“否否”一种投球方式,其概率为:P(1)=( )2=
)2=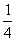 ,
,
∴P=P(3)+P(2)+P(1)+P(0)=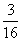 +
+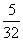 +
+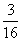 +
+ 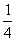 =
=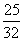 .
.
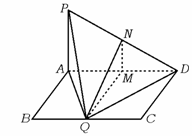
7、[思考] 这是一道探索性问题,解决这类问题常从要探求的线面关系必须满足的条件出发.此题要使PQ⊥QD,∵PA⊥面ABCD,只需满足AQ⊥QD即可,再转化到在平面ABCD上寻求AQ⊥QD的条件,从而使问题得到解决.
[解答] (1)连结AQ,∵PA⊥面ABCD.
∴要使PQ⊥QD,只要AQ⊥QD,即以AD为直径的圆与BC有公共点.
这就是说,当AD≥2AB,即a≥2,在BC边上存在点Q,使PQ⊥QD.
(2)∵当a>2时,以AD为直径的圆与BC有两个交点.
当a=2时,只有BC的中点满足条件.∴AD=2,Q为BC的中点,取AD的中点M,连结QM.
∵面PAD⊥面ABCD,QM⊥AD,∴QM⊥面PAD.过M作MN⊥PD于N,连结NQ.
根据三垂线定理有,QN⊥PD.∴∠MNQ就是二面角Q-PD-A的平面角.
在Rt△QMN中,QM=1,MN=MD·sin∠MDN=1×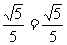 . ∴tan∠MNQ=
. ∴tan∠MNQ=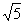 .
.
∴二面角Q-PD-A为arctan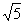 .
.
6、[解答]取3个小球的方法数为C =4060.
=4060.
设“3个小球全是红球”为事件A,“3个小球全是蓝球”为事件B,“3个小球全是黄球”为事件C,则P(B)=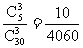 ,P(C)=
,P(C)=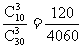 .
.
∵A、B、C为互斥事件,∴P(A+B+C)=P(A)+P(B)+P(C).
即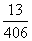 =P(A)+
=P(A)+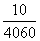 +
+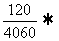 P(A)=0.∴红球的个数≤2,又∵n≥2,故n=2.
P(A)=0.∴红球的个数≤2,又∵n≥2,故n=2.
记“3个小球至少有一个是红球”为事件D,则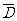 ?为“3个小球没有一个红球”.
?为“3个小球没有一个红球”.
 P(D)=1-P(
P(D)=1-P(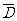 )=1
)=1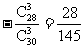 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com