
3、依次填入下列横线上的词语,最恰当的一组是( )
有位作家说,要想使自己的生活扁舟轻驶,务必要它____的仅限于必不可少之物,不然轻则____无以进,重则压沉自己的生活之舟。道理很明白,什么都舍不得撒手,往往____什么都不得不____。
A.装载 徜徉 致使 割爱
B.承载 徘徊 导致 舍弃
C.装载 徘徊 致使 舍弃
D.承载 徜徉 导致 割爱
2、依次填入下列横线上的词语,最恰当的一组是( )
1他____不决的伫立着,缓缓环顾四周的房屋和景物。
2他们学习了《中国教育改革和发展纲要》,决心统筹安排,因地制宜,____推进农村教育综合改革。
3为了躲避敌人的追捕,她____成一个阔太太,打扮的珠光宝气。
A. 犹豫 逐步 化装
B. 迟疑 逐渐 化妆
C. 迟疑 逐渐 化装
D. 犹豫 逐步 化妆
1、下列句子中加点的词语使用正确的一句是( )
A. 芦沟桥两边的石栏上雕刻着数以百计的石狮,这些石狮已守桥三百多个岁月。
B. 在今天举行的决赛中,我国选手有实力染指金牌的项目是女子一百米蝶泳和女子马拉松比赛。
C.他门门功课在班里名列前茅,还发表了几首小诗,可见文学造诣很深。
D.这家报纸改版后面貌一新,受到读者欢迎,很多报纸跟着仿效起来。
12.一天要排语文、数学、英语、生物、体育、班会六节课(上午四节,下午二节),要求上午第一节不排体育,数学课排在上午,班会课排在下午,问共有多少种不同的排课方法?
解法一:(从数学课排不排第一节入手)
(第一类)数学排在第一节,班会课排在下午,其余四科任排,得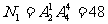
(第二类)数学排在上午另三节中的一节,班会排在下午,体育排在余下(不会第一节)三节中的一节,其余三科任排,得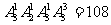
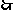 共有排法
共有排法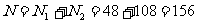 (种)
(种)
解法二(从体育课入手)
(第一类)体育课在上午 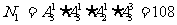
(第二类)体育课在下午 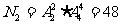
共有排法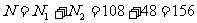 (种)
(种)
[探索题]三边长均为整数,且最大边长为11的三角形的个数是多少?
解:设较小的两边长为x、y且x≤y,
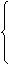 则
x≤y≤11,
则
x≤y≤11,
x+y>11,
x、y∈N*.
当x=1时,y=11;
当x=2时,y=10,11;
当x=3时,y=9,10,11;
当x=4时,y=8,9,10,11;
当x=5时,y=7,8,9,10,11;
当x=6时,y=6,7,8,9,10,11;
当x=7时,y=7,8,9,10,11;
……
当x=11时,y=11.
所以不同三角形的个数为
1+2+3+4+5+6+5+4+3+2+1=36.
评述:本题关键是列出约束条件,然后寻找x=1,2,…,11时,y的取值个数的规律,再用分类计数原理求解.
11.用1,2,3,4,5排成一个数字不重复的五位数a1a2a3a4a5,满足a1<a2,a2>a3,a3<a4,a4>a5的五位数有多少个?
解:因为a2>a1、a3,a4>a3、a5,所以a2只能是3、4、5.
(1)若a2=3,则a4=5,a5=4,a1与a3是1或2,这时共有A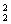 =2个符合条件的五位数.
=2个符合条件的五位数.
(2)若a2=4,则a4=5,a1、a3、a5可以是1、2、3,共有A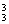 =6个符合条件的五位数.
=6个符合条件的五位数.
(3)若a2=5,则a4=3或4,此时分别与(1)(2)情况相同.
所以,满足条件的五位数有2(A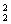 +A
+A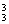 )=16个.
)=16个.
10.从数字0、1、3、5、7中取出不同的三个作系数,可组成多少个不同的一元二次方程ax2+bx+c=0?其中有实数根的有几个?
分析:(1)二次方程要求a不为0,故a只能在1、3、5、7中选,b、c没有限制.
(2)二次方程要有实根,需Δ=b2-4ac≥0,再对c分类讨论.
解:(1)a只能在1、3、5、7中选一个有A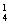 种,b、c可在余下的4个中任取2个,有A
种,b、c可在余下的4个中任取2个,有A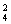 种.故可组成二次方程A
种.故可组成二次方程A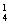 ·A
·A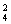 =48个.
=48个.
(2)方程要有实根,需Δ=b2-4ac≥0.
c=0,a、b可在1、3、5、7中任取2个,有A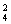 种;
种;
c≠0,b只能取5、7,b取5时,a、c只能取1、3,共有A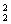 个;b取7时,a、c可取1、3或1、5,有2A
个;b取7时,a、c可取1、3或1、5,有2A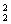 个.故有实根的二次方程共有A
个.故有实根的二次方程共有A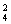 +A
+A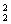 +2A
+2A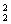 =18个.
=18个.
9.关于正整数2160,求:
(1)它有多少个不同的正因数?
(2)它的所有正因数的和是多少?
解:(1)∵N=2160=24×33×5,
∴2160的正因数为P=2α×3β×5γ,
其中α=0,1,2,3,4,β=0,1,2,3,γ=0,1.
∴2160的正因数共有5×4×2=40个.
(2)式子(20+21+22+23+24)×(30+31+32+33)×(50+51)的展开式就是40个正因数.
∴正因数之和为31×40×6=7440.
8.一只青蛙从正六边形ABCDEF的顶点A处起跳,每次可以跳到与它相邻的两个顶点之一,若5步内(含5步)跳到顶点D则停止,5步跳不到D点也停止,问共有多少种不同的跳法?
解法1:3步跳到D点的有2种方法。
5步跳到或跳不到D点的共有 25-2×22=24种方法,(其中2×22是3步跳到D后还继续跳的)。所以,共有不同跳法 2+24=26 (种)
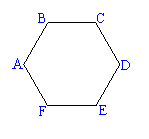
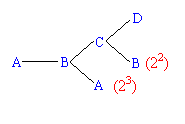 解法2:画树图
解法2:画树图
共有(1+22+23)×2=26(种)。
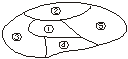
7.(2003年全国)如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色.现有4种颜色可供选择,则不同的着色方法共有_____________种.(以数字作答)
练习简答:1-3.BCC; 4..448; 5. 2400;.
6分首位是2、3、4分别计算:(1+C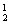 ·A
·A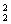 +C
+C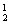 ·A
·A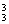 )+ A
)+ A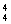 +C
+C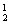 ·A
·A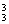 =58; 7.依次染①、②、③、④、⑤.故有4×3×2×(1+2)=72种.
=58; 7.依次染①、②、③、④、⑤.故有4×3×2×(1+2)=72种.
[解答题]
6.(2004四川模拟)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com