
3.一个酒杯的轴截面为抛物线的一部分,它的方程为
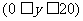 ,在杯内放一个玻璃球,要使球触及到杯的底部,则玻璃球的半径
,在杯内放一个玻璃球,要使球触及到杯的底部,则玻璃球的半径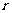 的范围为 ()
的范围为 ()
A 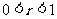 B
B 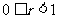 C
C 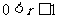 D
D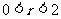
1.(2005全国)抛物线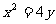 上一点A的纵坐标为4,则点A与抛物线焦点的距离为( )
上一点A的纵坐标为4,则点A与抛物线焦点的距离为( )
A.2 B.3 C.4 D.5
2
已知点 F是抛物线
F是抛物线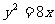 的焦点,M是抛物线上的动点,当
的焦点,M是抛物线上的动点,当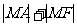 最小时,M点坐标是 ( )
最小时,M点坐标是 ( )
A
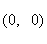 B
B 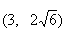 C
C  D
D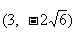
3.解决焦点弦问题时,应注意抛物线的定义和焦点弦的几何性质应用,注意抛物线上的点,焦点,,准线三者之间的联系.
同步练习 8.3抛物线方程及性质
[选择题]
2.涉及抛物线的弦长、弦的中点、弦的斜率问题时,要注意运用“设而不求”的策略,避免求交点坐标的复杂运算.
1.求抛物线方程的方法:待定系数法,定义法,直接法;
4.特别注意范围的限定.
[例4](2005全国卷Ⅲ)设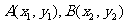 两点在抛物线
两点在抛物线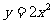 上,l是AB的垂直平分线.
上,l是AB的垂直平分线.
(Ⅰ)当且仅当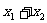 取何值时,直线l经过抛物线的焦点F?证明你的结论;
取何值时,直线l经过抛物线的焦点F?证明你的结论;
(Ⅱ)当直线l的斜率为2时,求l在y轴上截距的取值范围.
解:(Ⅰ)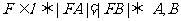 两点到抛物线的准线的距离相等.
两点到抛物线的准线的距离相等.
∵抛物线的准线是x轴的平行线, 不同时为0,
不同时为0,
∴上述条件等价于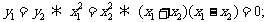
∵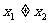 , ∴上述条件等价于
, ∴上述条件等价于 
即当且仅当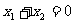 时,l经过抛物线的焦点F.
时,l经过抛物线的焦点F.
另解:(Ⅰ)∵抛物线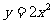 ,即
,即 ,
,
∴焦点为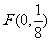
(1)直线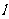 的斜率不存在时,显然有
的斜率不存在时,显然有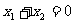
(2)直线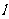 的斜率存在时,设为k, 截距为b
的斜率存在时,设为k, 截距为b
即直线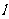 :y=kx+b
由已知得:
:y=kx+b
由已知得:
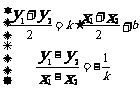
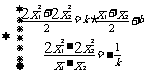
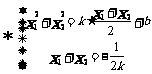

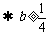
即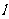 的斜率存在时,不可能经过焦点
的斜率存在时,不可能经过焦点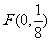
所以当且仅当 =0时,直线
=0时,直线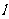 经过抛物线的焦点F
经过抛物线的焦点F
(II)(理)设l在y轴上的截距为b,依题意得l的方程为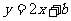 ;过点A、B的直线方程可写为
;过点A、B的直线方程可写为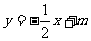 ,所以
,所以 满足方程
满足方程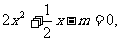 得
得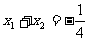 ;
;
A,B为抛物线上不同的两点等价于上述方程的判别式
即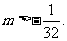
设AB的中点N的坐标为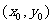 ,则
,则

由
即得l在y轴上截距的取值范围为(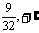 ).
).
法二:y1=2x12, y2=2x22, 相减得

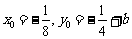 ,
,
中点在抛物线内必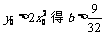
[研讨.欣赏](2005山东文)
已知动圆过定点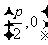 ,且与直线
,且与直线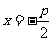 相切,其中
相切,其中 .
.
(I)求动圆圆心 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹 上异于原点
上异于原点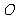 的两个不同点,直线
的两个不同点,直线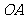 和
和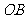 的倾斜角分别为
的倾斜角分别为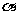 和
和 ,当
,当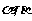 变化且
变化且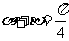 时,证明直线
时,证明直线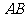 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.


解:(I)如图,设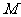 为动圆圆心,
为动圆圆心,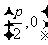 为记为
为记为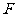 ,过点
,过点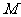 作直线
作直线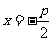 的垂线,垂足为
的垂线,垂足为 ,由题意知:
,由题意知: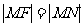 即动点
即动点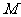 到定点
到定点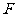 与定直线
与定直线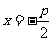 的距离相等,由抛物线的定义知,点
的距离相等,由抛物线的定义知,点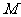 的轨迹为抛物线,其中
的轨迹为抛物线,其中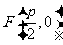 为焦点,
为焦点,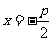 为准线,所以轨迹方程为
为准线,所以轨迹方程为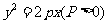
(II)如图,设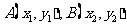 ,由题意得
,由题意得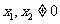 。又直线
。又直线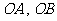 的倾斜角
的倾斜角 满足
满足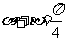 ,故
,故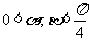 。∴直线
。∴直线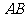 的斜率存在,否则,
的斜率存在,否则,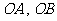 的倾斜角
的倾斜角 。从而设直线
。从而设直线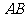 的方程为
的方程为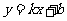 ,显然
,显然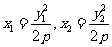 ,将
,将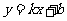 与
与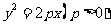
联立消去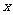 ,得
,得 由韦达定理知
由韦达定理知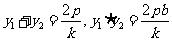 ①
①
由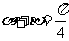 ,得
,得
 。将①式代入上式整理化简,得
。将①式代入上式整理化简,得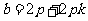 :此时直线
:此时直线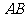 的方程可表示为:
的方程可表示为: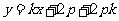 ,即
,即 。∴直线
。∴直线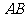 恒过定点
恒过定点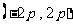
3.运用距离公式求出标准方程中的待定系数;
2.合理选择坐标系,确定标准方程;
[例1]给定抛物线y2=2x,设A(a,0),a>0,P是抛物线上的一点,且|PA|=d,试求d的最小值.
解:设P(x0,y0)(x0≥0),则y02=2x0,
∴d=|PA|=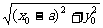
=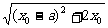 =
=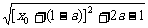 .
.
∵a>0,x0≥0,
∴(1)当0<a<1时,1-a>0,
此时有x0=0时,dmin=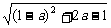 =a.
=a.
(2)当a≥1时,1-a≤0,
此时有x0=a-1时,dmin=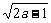 .
.
[例2]过抛物线y2=2px(p>0)焦点F的弦AB,点A、B在抛物线准线上的射影为A1、B1,求∠A1FB1.
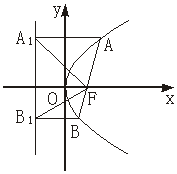
解法1:由抛物线定义及平行线性质知∠A1FB1=180°-(∠AFA1+∠BFB1)
=180°- (180°-∠A1AF)-
(180°-∠A1AF)- (180°-∠B1BF)
(180°-∠B1BF)
= (∠A1AF+∠B1BF)=90°.
(∠A1AF+∠B1BF)=90°.
法2:设弦AB的方程是: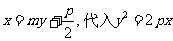
得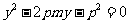 ,
,
设A(x1,y1),B(x2,y2),由韦达定理得y1y2= -p2
又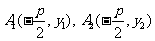 ,
,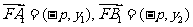
∴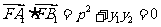 从而知∠A1FB1=90°.
从而知∠A1FB1=90°.
提炼方法: 1.平面几何法与定义法结合,简捷高效;
2.
弦AB的方程是: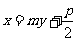 (本题不存在AB垂直于y轴的情况),避开了斜率存在性的讨论,解题中应注意灵活运用.
(本题不存在AB垂直于y轴的情况),避开了斜率存在性的讨论,解题中应注意灵活运用.
[例3] 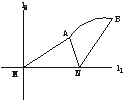 如下图所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1,以A、B为端点的曲线段C上任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如下图所示,直线l1和l2相交于点M,l1⊥l2,点N∈l1,以A、B为端点的曲线段C上任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=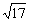 ,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
解:以直线l1为x轴,线段MN的垂直平分线为y轴,建立直角坐标系,由条件可知,曲线段C是以点N为焦点,以l2为准线的抛物线的一段.其中A、B分别为曲线段C的端点.
设曲线段C的方程为y2=2px(p>0)(xA≤x≤xB,y>0),其中xA、xB为A、B的横坐标,p=|MN|,
所以M(- ,0)
、N(
,0)
、N( ,0).
,0).
由|AM|=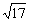 ,|AN|=3,得
,|AN|=3,得
(xA+ )2+2pxA=17, ①
)2+2pxA=17, ①
(xA- )2+2pxA=9. ②
)2+2pxA=9. ②
①②联立解得xA=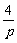 ,代入①式,并由p>0,
,代入①式,并由p>0,
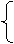
|
|
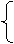 p=4, p=2,
p=4, p=2,
xA=1 xA=2.
因为△AMN为锐角三角形,所以 >xA.
>xA.
|
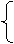
|
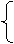 P=2, P=4,
P=2, P=4,
xA=2. xA=1.
由点B在曲线段C上,得xB=|BN|- =4.
=4.
综上,曲线段C的方程为y2=8x(1≤x≤4,y>0).
提炼方法: 1.熟练运用定义确定曲线C是抛物线段;
5.把点A的坐标(0,9)代入y=ax2+c得c=9,即运动物体的轨迹方程为y=ax2+9.
令y=0,得ax2+9=0,即x2=-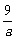 .
.
若物体落在D内,应有6<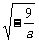 <7,
<7,
解得- <a<-
<a<-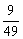 . 6.N(x0+4,
0)
. 6.N(x0+4,
0)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com