
9.(本小题满分14分)(2005年春考·北京卷·理18)
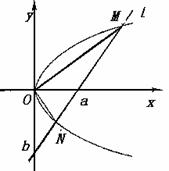 如图,O为坐标原点,直线
如图,O为坐标原点,直线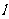 在
在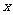 轴和
轴和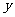 轴上的截距分别是
轴上的截距分别是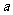 和
和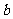 ,且交抛物线
,且交抛物线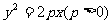 于
于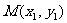 、
、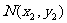 两点.
两点.
(1)写出直线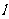 的截距式方程;
的截距式方程;
(2)证明: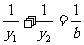 ;
;
(3)当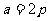 时,求
时,求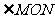 的大小.
的大小.
(Ⅰ)解:直线l的截距式方程为  ①
①
(Ⅱ)证明:由①及y2=2px消去x可得
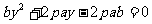 ②
②
点M,N的纵坐标y1, y2为②的两个根,故

(Ⅲ)解:设OM,ON的斜率分别为k1,k2,

8.(本小题满分14分)(2005年高考·广东卷17)
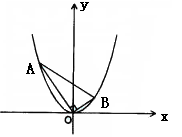 在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图4所示).
在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图4所示).
(Ⅰ)求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)△AOB的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
解:(I)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2), 则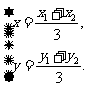 …(1)
…(1)
∵OA⊥OB,即 , ……(2)
, ……(2)
又点A,B在抛物线上,有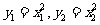 ,代入(2)化简得
,代入(2)化简得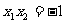
∴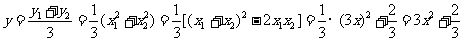 ,
,
所以重心为G的轨迹方程为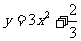 .
.
(II)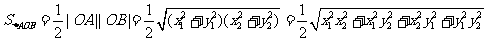
由(I)得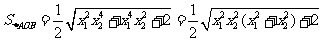

当且仅当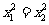 即
即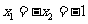 时,
时,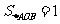 .
.
所以△AOB的面积存在最小值,且最小值为1.
7.(2005春北京文)
如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2, y2)两点.
(1)求x1x2与y1y2的值;
(2)求证:OM⊥ON.
(Ⅰ)解:直线l的方程为
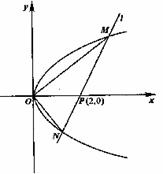
 ①
①
代入y2=2x消去y可得
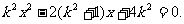 ②
②
点M,N的横坐标x1与 x2是②的两个根,
由韦达定理得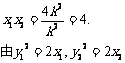
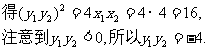
(Ⅱ)证明:设OM,ON的斜率分别为k1, k2,

6.由抛物线方程y2=10x可知②⑤满足条件.答案:②⑤
[解答题]
5.可证弦AB通过焦点F时,所求距离最短,答案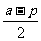
4.向量解法: 由A、F、B共线得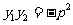 (重要结论),进而得出
(重要结论),进而得出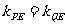
3. 设圆心A(0,t),抛物线上的点为P(x,y), 列出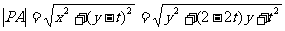 转化为二次函数问题。
转化为二次函数问题。
6.对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;②焦点在x轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④抛物线的通径的长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).
能使这抛物线方程为y2=10x的条件是____________.(要求填写合适条件的序号)
简答提示:1-4:DCCC;2. 把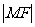 转化为M到准线的距离
转化为M到准线的距离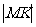 ,然后求
,然后求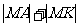 的最小值
的最小值
5.抛物线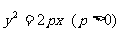 的动弦AB长为
的动弦AB长为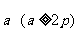 ,则AB中点M到
,则AB中点M到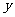 轴的最短距离是 ________
轴的最短距离是 ________
4. 设抛物线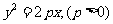 的轴和它的准线交于E点,经过焦点F的直线交抛物线于P、Q两点(直线PQ与抛物线的轴不垂直),则
的轴和它的准线交于E点,经过焦点F的直线交抛物线于P、Q两点(直线PQ与抛物线的轴不垂直),则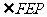 与
与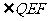 的大小关系为 ( )
的大小关系为 ( )
A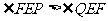 B
B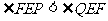
C 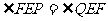 D 不确定
D 不确定
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com