
1)使用高倍显微镜观察几种细胞,比较不同细胞的异同点
2)运用制作临时装片的方法
(一)可溶性糖的鉴定
|
操 作 方 法 |
注 意 问 题 |
解 释 |
|
1. 制备组织样液。 (去皮、切块、研磨、过滤) |
苹果或梨组织液必须临时制备。 |
因苹果多酚氧化酶含量高,组织液很易被氧化成褐色,将产生的颜色掩盖。 |
|
2. 取1支试管,向试管内注入2mL组织样液。 |
|
|
|
3. 向试管内注入1mL新制的斐林试剂,振荡。 |
应将组成斐林试剂的甲液、乙液分别配制、储存,使用前才将甲、乙液等量混匀成斐林试剂; 切勿将甲液、乙液分别加入苹果组织样液中进行检测。 |
斐林试剂很不稳定,甲、乙液混合保存时,生成的Cu ( OH ) 2在70~900C下分解成黑色CuO和水; 甲、乙液分别加入时可能会与组织样液发生反应,无Cu ( OH ) 2生成。 |
|
4. 试管放在盛有50-650C温水的大烧杯中,加热约2分钟,观察到溶液颜色:浅蓝色 → 棕色 → 砖红色(沉淀) |
最好用试管夹夹住试管上部,使试管底部不触及烧杯底部,试管口不朝向实验者。 也可用酒精灯对试管直接加热。 |
防止试管内的溶液冲出试管,造成烫伤; 缩短实验时间。 |
(二)脂肪的鉴定
|
操 作 方 法 |
注 意 问 题 |
解 释 |
|
花生种子浸泡、去皮、切下一些子叶薄片,将薄片放在载玻片的水滴中,用吸水纸吸去装片中的水。 |
干种子要浸泡3~4小时,新花生的浸泡时间可缩短。 |
因为浸泡时间短,不易切片,浸泡时间过长,组织较软,切下的薄片不易成形。切片要尽可能薄些,便于观察。 |
|
在子叶薄片上滴2~3滴苏丹Ⅲ或苏丹Ⅳ染液,染色1分钟。 |
染色时间不宜过长。 |
|
|
用吸水纸吸去薄片周围染液,用50%酒精洗去浮色,吸去酒精。 |
|
酒精用于洗去浮色,不洗去浮色,会影响对橘黄色脂肪滴的观察。同时,酒精是脂溶性溶剂,可将花生细胞中的脂肪颗粒溶解成油滴。 |
|
用吸水纸吸去薄片周围酒精,滴上1~2滴蒸馏水,盖上盖玻片。 |
|
滴上清水可防止盖盖玻片时产生气泡。 |
|
低倍镜下找到花生子叶薄片的最薄处,可看到细胞中有染成橘黄色或红色圆形小颗粒。 |
装片不宜久放。 |
时间一长,油滴会溶解在乙醇中。 |
三、蛋白质的鉴定
|
操 作 方 法 |
注 意 问 题 |
解 释 |
|
制备组织样液。 (浸泡、去皮研磨、过滤。) |
|
黄豆浸泡1至2天,容易研磨成浆,也可购新鲜豆浆以节约实验时间。 |
|
鉴定。加样液约2ml于试管中,加入双缩脲试剂A,摇匀;再加入双缩脲试剂B液3~4滴,摇匀,溶液变紫色。 |
A液和B液也要分开配制,储存。鉴定时先加A液后加B液。 CuSO4溶液不能多加。 |
先加NaOH溶液,为Cu2+与蛋白质反应提供一个碱性的环境。A、B液混装或同时加入,会导致Cu2+变成Cu ( OH ) 2沉淀,而失效。 否则CuSO4的蓝色会遮盖反应的真实颜色。 |
|
可用蛋清代替豆浆。 |
蛋清要先稀释。 |
如果稀释不够,在实验中蛋清粘在试管壁,与双缩脲试剂反应后会粘固在试管内壁上,使反应不容易彻底,并且试管也不易洗干净。 |
|
附:淀粉的检测和观察 用试管取2ml待测组织样液,向试管内滴加2滴碘液,观察颜色变化。 |
碘液不要滴太多 |
以免影响颜色观察 |
实验三 用显微镜观察多种多样的细胞(必修一P7)
斐林试剂(包括甲液:质量浓度为0.1g/ mL NaOH溶液和乙液:质量浓度为0.05g/ mL CuSO4溶液)、苏丹Ⅲ或苏丹Ⅳ染液、双缩脲试剂(包括A液:质量浓度为0.1g/ mL NaOH溶液和B液:质量浓度为0.01g/ mL CuSO4溶液)、体积分数为50%的酒精溶液,碘液、蒸馏水。
3.做蛋白质的鉴定实验,可用富含蛋白质的黄豆或鸡蛋清。
2.做脂肪的鉴定实验。应选富含脂肪的种子,以花生种子为最好,实验前一般要浸泡3~4小时(也可用蓖麻种子)。
1.做可溶性还原性糖鉴定实验,应选含糖高,颜色为白色的植物组织,如苹果、梨。(因为组织的颜色较浅,易于观察。)
3.蛋白质与双缩脲试剂发生作用,产生紫色反应。(蛋白质分子中含有很多肽键,在碱性NaOH溶液中能与双缩脲试剂中的Cu2+作用,产生紫色反应。)
2.脂肪可以被苏丹Ⅲ染液染成橘黄色(或被苏丹Ⅳ染液染成红色)。淀粉遇碘变蓝色。
1.可溶性还原糖(如葡萄糖、果糖、麦芽糖)与斐林试剂发生作用,可生成砖红色的Cu 2O沉淀。如:
|
 葡萄糖+ Cu ( OH ) 2 葡萄糖酸
+ Cu 2O↓(砖红色)+ H 2O,即Cu ( OH ) 2被还原成Cu 2O,葡萄糖被氧化成葡萄糖酸。
葡萄糖+ Cu ( OH ) 2 葡萄糖酸
+ Cu 2O↓(砖红色)+ H 2O,即Cu ( OH ) 2被还原成Cu 2O,葡萄糖被氧化成葡萄糖酸。10.(2000春全国)已知抛物线y2=4px(p>0),O为顶点,A、B为抛物线上的两动点,且满足OA⊥OB,如果OM⊥AB于M点,求点M的轨迹方程.
分析:点M随着A、B两点的变化而变化,点M是OM与AB的交点,而A、B为抛物线上的动点,点M与A、B的直接关系不明显,因此需引入参数.
解法一:设M(x0,y0),则kOM= ,kAB=-
,kAB=-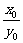 ,
,
直线AB方程是y=-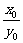 (x-x0)+y0.
(x-x0)+y0.
由y2=4px可得x= ,代入上式整理得
,代入上式整理得
x0y2-(4py0)y-4py02-4px02=0. ①
此方程的两根y1、y2分别是A、B两点的纵坐标,
∴A(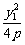 ,y1)、B(
,y1)、B( ,y2).
,y2).
∵OA⊥OB,∴kOA·kOB=-1.
∴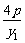 ·
· =-1.∴y1y2=-16p2.
=-1.∴y1y2=-16p2.
根据根与系数的关系,由①可得
y1·y2= ,
,
∴ =16p2.
=16p2.
化简,得x02+y02-4px0=0,
即x2+y2-4px=0(除去原点)为所求.
∴点M的轨迹是以(2p,0)为圆心,以2p为半径的圆,去掉坐标原点.
解法二:设M(x,y),直线AB方程为y=kx+b,
由OM⊥AB得k=- .
.
由y2=4px及y=kx+b消去y,得
k2x2+x(2kb-4p)+b2=0.
所以x1x2= .消去x,得ky2-4py+4pb=0.
.消去x,得ky2-4py+4pb=0.
所以y1y2=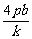 .由OA⊥OB,
.由OA⊥OB,
得y1y2=-x1x2,
所以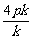 =-
=- ,b=-4kp.
,b=-4kp.
故y=kx+b=k(x-4p).
用k=- 代入,得
代入,得
x2+y2-4px=0(x≠0).
解法三:设点M的坐标为(x,y),直线OA的方程为y=kx,
|
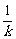 x.
x.
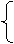
|
y2=4px,
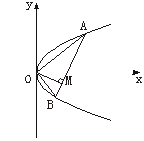 类似地可得B点的坐标为(4pk2,-4pk),
类似地可得B点的坐标为(4pk2,-4pk),
从而知当k≠±1时,
kAB=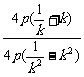 =
= .
.
故得直线AB的方程为y+4pk= (x-4pk2),
(x-4pk2),
即(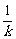 -k)y+4p=x,
①
-k)y+4p=x,
①
直线OM的方程为y=-(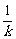 -k)x. ②
-k)x. ②
可知M点的坐标同时满足①②,
由①及②消去k便得4px=x2+y2,
即(x-2p)2+y2=4p2,但x≠0,
当k=±1时,容易验证M点的坐标仍适合上述方程.
故点M的轨迹方程为(x-2p)2+y2=4p2(x≠0),
它表示以点(2p,0)为圆心,以2p为半径的圆.
[探索题](2006辽宁)
已知点 ,
,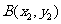
 是抛物线
是抛物线 上的两个动点,
上的两个动点,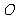 是坐标原点,向量
是坐标原点,向量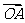 ,
,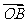 满足
满足 .设圆
.设圆 的方程为
的方程为
(I)证明线段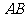 是圆
是圆 的直径;
的直径;
(II)当圆C的圆心到直线x-2y=0的距离的最小值为 时,求P的值。
时,求P的值。
(I)证法一:∵ ,
,
∴ ,
,
即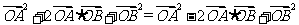 ,
,
整理得 .
.
∴ 1
1
设点 是以线段
是以线段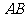 为直径得圆上得任意一点,则
为直径得圆上得任意一点,则
即
展开上式并将1带入得
故线段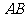 是圆
是圆 的直径.
的直径.
证法二:同法一得: 1
1
以 AB 为直径的圆的方程是
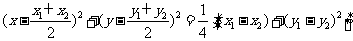 ,
,
展开,并将①代入得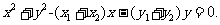
所以线段 AB 是圆 C 的直径
(II)解法一:设圆 的圆心为
的圆心为 则
则
∵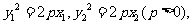
∴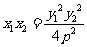
又∵ =0
=0
∴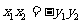 ∴
∴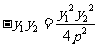
∵ ,∴
,∴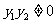 , ∴
, ∴
∴
 ,
,
所以圆心的轨迹方程为: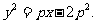
设圆心 到直线
到直线 的距离为
的距离为 ,则
,则

当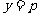 时,
时, 有最小值
有最小值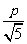 ,由题设得
,由题设得 ,∴
,∴
解法二:同法一得:圆心的轨迹方程为: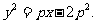
设直线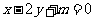 与
与 的距离为
的距离为 ,则
,则

当 与
与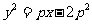 仅有一个公共点时,
仅有一个公共点时,
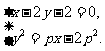 该点到
该点到 的距离最小,最小值为
的距离最小,最小值为 ,
,
由 ②
③
消x得 ,
,
由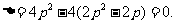
得 (∵
(∵ )
)
解法三:设圆 的圆心为
的圆心为 ,则
,则
若圆心 到直线
到直线 的距离为
的距离为 ,那
,那
∵
∴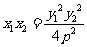
又∵ ,
, 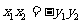 ,
,
∵ ,∴
,∴
∴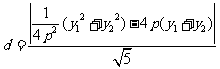
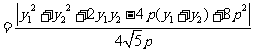

当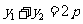 时,
时, 有最小值
有最小值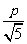 ,由题设得
,由题设得 ,
,
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com