
2.(2009年广东理19)(本小题满分14分)
已知曲线 与直线
与直线 交于两点
交于两点 和
和 ,且
,且 .记曲线
.记曲线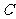 在点
在点 和点
和点 之间那一段
之间那一段 与线段
与线段 所围成的平面区域(含边界)为
所围成的平面区域(含边界)为 .设点
.设点 是
是 上的任一点,且点
上的任一点,且点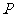 与点
与点 和点
和点 均不重合.
均不重合.
(1)若点 是线段
是线段 的中点,试求线段
的中点,试求线段 的中点
的中点 的轨迹方程;
的轨迹方程;
(2)若曲线 与
与 有公共点,试求
有公共点,试求 的最小值.
的最小值.
 解:(1)联立
解:(1)联立 与
与 得
得 ,则
,则 中点
中点 ,设线段
,设线段 的中点
的中点 坐标为
坐标为 ,则
,则 ,即
,即 ,又点
,又点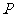 在曲线
在曲线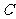 上,
上,
∴ 化简可得
化简可得 ,又点
,又点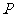 是
是 上的任一点,且不与点
上的任一点,且不与点 和点
和点 重合,则
重合,则 ,即
,即 ,∴中点
,∴中点 的轨迹方程为
的轨迹方程为 (
( ).
).
(2)曲线 ,即圆
,即圆 :
: ,其圆心坐标为
,其圆心坐标为 ,半径
,半径 由图可知,当
由图可知,当 时,曲线
时,曲线 与点
与点 有公共点;当
有公共点;当 时,要使曲线
时,要使曲线 与点
与点 有公共点,只需圆心
有公共点,只需圆心 到直线
到直线 的距离
的距离 ,得
,得 ,则
,则 的最小值为
的最小值为 .
.
1.( 2009年江苏22)(本题满分10分)
2009年江苏22)(本题满分10分)
在平面直角坐标系 中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在
中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在 轴上。
轴上。
(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点 的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为
的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为 ,求
,求 关于
关于 的表达式。
的表达式。
[解析] 本小题主要考查直线、抛物线及两点间的距离公式等基本知识,考查运算求解能力。满分10分。



7.(2007年广东理11)在直角坐标系xOy中,有一定点A(2,1)。若线段OA的垂直平分线过抛物线 的焦点,则该抛物线的准线方程是______;
的焦点,则该抛物线的准线方程是______;
答案: ;解析:OA的垂直平分线的方程是y-
;解析:OA的垂直平分线的方程是y- ,令y=0得到x=
,令y=0得到x= ;
;
6.(2007年山东理13)设 是坐标原点,
是坐标原点, 是抛物线
是抛物线 的焦点,
的焦点, 是抛物线上的一点,
是抛物线上的一点, 与
与 轴正向的夹角为
轴正向的夹角为 ,则
,则 为________.
为________.
[答案]:  [分析]:过A 作
[分析]:过A 作 轴于D,令
轴于D,令 ,则
,则 ,
, ,
, 。
。
5.(2009年福建理13)过抛物线 的焦点F作倾斜角为
的焦点F作倾斜角为 的直线交抛物线于A、B两点,若线段AB的长为8,则
的直线交抛物线于A、B两点,若线段AB的长为8,则 ________________
________________


[答案]:2解析:由题意可知过焦点的直线方程为 ,联立有
,联立有 ,又
,又 。
。
4.(2009年海南理13)设已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A,B两点。若AB的中点为(2,2),则直线 的方程为_____________.
的方程为_____________.
答案:y=x解析:抛物线的方程为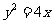 ,
,

3.(2010年上海理3) 动点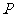 到点
到点 的距离与它到直线
的距离与它到直线 的距离相等,则
的距离相等,则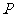 的轨迹方程为
。
的轨迹方程为
。
解析:考查抛物线定义及标准方程
定义知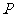 的轨迹是以
的轨迹是以 为焦点的抛物线,p=2所以其方程为y2=8x
为焦点的抛物线,p=2所以其方程为y2=8x
2.(2010年浙江理13)设抛物线 的焦点为
的焦点为 ,点
,点 .若线段
.若线段 的中点
的中点 在抛物线上,则
在抛物线上,则 到该抛物线准线的距离为_____________。
到该抛物线准线的距离为_____________。
解析:利用抛物线的定义结合题设条件可得出p的值为 ,B点坐标为(
,B点坐标为( )所以点B到抛物线准线的距离为
)所以点B到抛物线准线的距离为 ,本题主要考察抛物线的定义及几何性质,属容易题
,本题主要考察抛物线的定义及几何性质,属容易题
1.(2010年湖南理14)过抛物线 的焦点作斜率为1的直线与该抛物线交于
的焦点作斜率为1的直线与该抛物线交于 两点,
两点, 在
在 轴上的正射影分别为
轴上的正射影分别为 .若梯形
.若梯形 的面积为
的面积为 ,则
,则 .
.
[答案]2
6.(2007年海南理6)已知抛物线 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 , 则有( )
, 则有( )
A. B.
B.
C. D.
D.
[答案]:C[分析]:由抛物线定义, 即:
即:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com