
10. 设a、b、c均为实数,求证: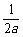 +
+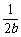 +
+ ≥
≥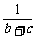 +
+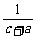 +
+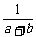 .
.
证明:∵a、b、c均为实数,
∴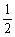 (
(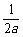 +
+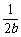 )≥
)≥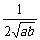 ≥
≥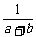 ,当a=b时等号成立;
,当a=b时等号成立;
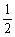 (
(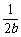 +
+ )≥
)≥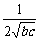 ≥
≥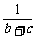 ,当b=c时等号成立;
,当b=c时等号成立;
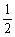 (
( +
+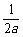 )≥
)≥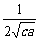 ≥
≥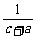 .
.
三个不等式相加即得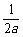 +
+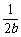 +
+ ≥
≥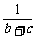 +
+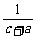 +
+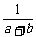 ,当且仅当a=b=c时等号成立.
,当且仅当a=b=c时等号成立.
[探索题](1).已知a3+b3=1,求a+b的取值范围.
(2) 已知a>0,b>0,a+b=4,求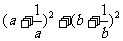 的最小值.
的最小值.
解(1) 易知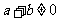 ,否则a=-b代入a3+b3=0与已知矛盾.
,否则a=-b代入a3+b3=0与已知矛盾.
令a+b=t≠0,由1=(a+b)3-3ab(a+b),得
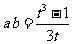 ,视a,b为方程
,视a,b为方程 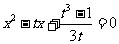 的根,
的根,
由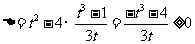 ,得
,得
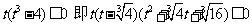 ①
①
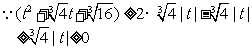
∴①为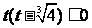
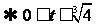
∴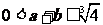
(2) 由4=a+b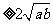 得ab≤4.
得ab≤4.
∴
当且仅当a=b时取“=”,所求最小值为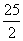 .
.
易错解:原式 ,最小值为8.
,最小值为8.
9.某种生产设备购买时费用10万元,每年的设备管理费共计9千元,这种生产设备的维修费各年为:第一年2千元,第二年4千元,第三年6千元,依每年2千元的增量逐年递增,问这种生产设备最多使用多少年报废最合算?(即年平均费用最少)
解:设使用x年的年平均费用为y(万元),则
y= ≥1+2
≥1+2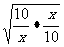 =3,
=3,
当且仅当x=10时,等号成立.
8.(1)若x>0,y>0,x+y=1,
求证:(1+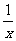 )(1+
)(1+ )≥9
)≥9
(2)设实数x,y满足y+x2=0,0<a<1,求证: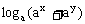 ≤
≤ 。
。
证明:(1)法一: 左边=(1+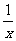 )(1+
)(1+ )=1+
)=1+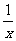 +
+ +
+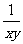 =1+
=1+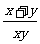 +
+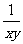
=1+ ≥1+
≥1+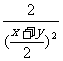 =9=右边 (当且仅当x=y=
=9=右边 (当且仅当x=y=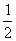 时取“=”号)
时取“=”号)
法二: 令x=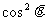 y=
y=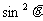 , 0<
, 0<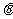 <
<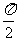
左边=(1+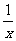 )(1+
)(1+ )=(1+
)=(1+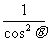 )(1+
)(1+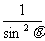 )
)
=1+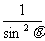 +
+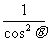 +
+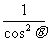 ·
·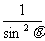 =1+
=1+
=1+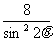 ≥1+8=9=右边
≥1+8=9=右边
0<2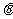 <
<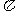
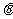 =
=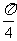 时,x=y=
时,x=y=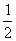 时取等号
时取等号
法三:∵x+y=1
∴左边=(1+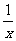 )(1+
)(1+ )=(1+
)=(1+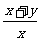 )(1+
)(1+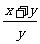 )=(2+
)=(2+ )(2+
)(2+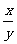 )
)
=5+2( +
+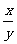 )≥5+4=9=右边 (当且仅当x=y=
)≥5+4=9=右边 (当且仅当x=y=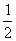 时取“=”号)
时取“=”号)
(2)∵ 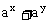 ≥
≥ ,
,
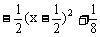 ≤
≤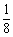 ,0<a<1
,0<a<1
∴  ≥
≥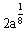 ∴
∴ 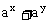 ≥
≥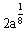
∴ 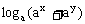 ≤
≤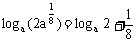
7. 设x≥0, y≥0, x2+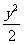 =1,求
=1,求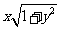 的最大值.
的最大值.
解法一: ∵x≥0, y≥0, x2+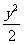 =1
=1
∴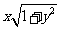 =
=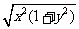 =
=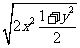
≤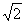
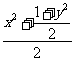 =
=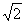
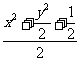 =
=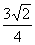
当且仅当x=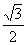 ,y=
,y=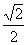 (即x2=
(即x2= 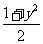 )时,
)时, 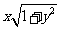 取得最大值
取得最大值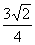
解法二: 令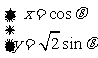 (0≤
(0≤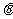 ≤
≤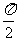 )
)
则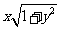 =cos
=cos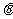
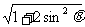 =
=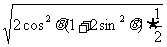
≤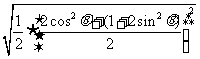 =
=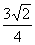
当 =
=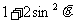 ,
,
即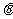 =
= 时,x=
时,x=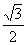 ,y=
,y=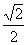 时,
时,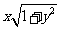 取得最大值
取得最大值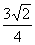
6.若x,y是正数,则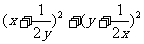 的最小值是_______
的最小值是_______
简答.提示:1-4.BBBB; 5. ②③; 6.原式=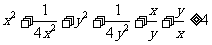
[解答题]
5. 下列不等式中恒成立的是_________
①ctgθ+tgθ≥2
②x+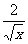 -1≥2
-1≥2
③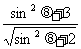 ≥2 ④xyz≤
≥2 ④xyz≤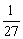 (x+y+z=1)
(x+y+z=1)
4.(2004全国I)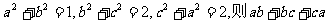 的最小值为( )
的最小值为( )
A.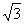 -
-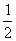 B.
B.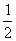 -
-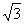 C.-
C.-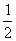 -
-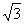 D.
D.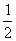 +
+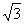
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com