
3.复数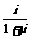 在复平面中所对应的点到原点的距离为( )
在复平面中所对应的点到原点的距离为( )
A.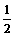 B.1
C.
B.1
C.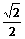 D.
D.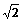
2.已知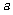 、
、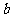 为实数,则
为实数,则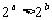 是
是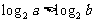 的( )
的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既不充分也不必要条件
1.若集合M={4,5,7,9},N={3,4,7,8,9},全集U=M∪N,则集合CU(M∩N) 中的元素共有( )
A. 3个 B . 4个 C . 5个 D . 6个
24.选修4-5:不等式选讲
设函数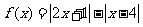 .
.
(1)解不等式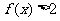 ;
;
(2)求函数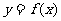 的最小值.
的最小值.
23.选修4-4:坐标系与参数方程
已知曲线C1的极坐标方程为 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为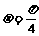 (
(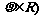 ,曲线C1,C2相交于点A,B。
,曲线C1,C2相交于点A,B。
(1)将曲线C1,C2的极坐标方程化为直角坐标方程;
(2)求弦AB的长。
22.选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,AH=2。
(1)求DE的长;
(2)延长ED到P,过P作圆O的切线,
切点为C,若PC=2 ,求PD的长。
,求PD的长。
21.(本小题满分12分)
已知函数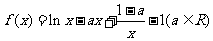
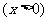
(1)当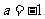 时,求曲线
时,求曲线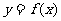 在点
在点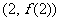 处的切线方程;
处的切线方程;
(2)当 时,讨论
时,讨论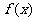 的单调性
的单调性
20.(本小题满分12分)
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=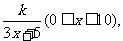 若不建隔热层,每年能源消耗费用为8万元。设
若不建隔热层,每年能源消耗费用为8万元。设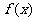 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。
(1)求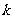 的值及
的值及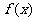 的表达式。
的表达式。
(2)隔热层修建多厚时,总费用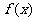 达到最小,并求最小值。
达到最小,并求最小值。
19.(本小题满分12分)
在△ABC中,内角A、B、C对边长分别是a,b,c,已知c=2,C=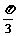
(1)若△ABC的面积等于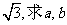 ;
;
(2)若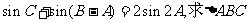 的面积。
的面积。
18.(本小题满分12分)
设{an}是等差数列,{bn}是各项为正项的等比数列,且a1=b1=1, a3+b5=21, a5+b3=13.
(1)求{an}, {bn}的通项公式;
(2)求数列{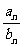 }的前n项和Sn;
}的前n项和Sn;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com